
【题目】两城市![]() 和
和![]() 相距
相距![]() ,现计划在两城市外以
,现计划在两城市外以![]() 为直径的半圆
为直径的半圆![]() 上选择一点
上选择一点![]() 建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城
建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城![]() 和城
和城![]() 的总影响度为城
的总影响度为城![]() 和城
和城![]() 的影响度之和,记
的影响度之和,记![]() 点到城
点到城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理场对城
处的垃圾处理场对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() ,统计调查表明:垃圾处理场对城
,统计调查表明:垃圾处理场对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为4,对城
的距离的平方成反比,比例系数为4,对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为
的距离的平方成反比,比例系数为![]() ,当垃圾处理场建在
,当垃圾处理场建在![]() 的中点时,对城
的中点时,对城![]() 和城
和城![]() 的总影响度为0.065;
的总影响度为0.065;
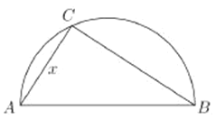
(1)将![]() 表示成
表示成![]() 的函数;
的函数;
(2)判断![]() 上是否存在一点,使建在此处的垃圾处理场对城
上是否存在一点,使建在此处的垃圾处理场对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,说明理由;
的距离;若不存在,说明理由;
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】东莞的轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内(含4小时)每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内(含24小时)收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间(假设每辆车一天内在该停车场仅停车一次),得到下面的频数分布表:
|
|
|
|
|
|
|
频数(车次) | 100 | 100 | 200 | 200 | 350 | 50 |
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
(1)现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的![]() 列联表:
列联表:
男 | 女 | 合计 | |
不超过6小时 | 30 | ||
6小时以上 | 20 | ||
合计 | 100 |
完成上述列联表,并判断能否有90%的把握认为“停车是否超过6小时”与性别有关?
(2)(i)![]() 表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求
表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求![]() 的概率分布列及期望
的概率分布列及期望![]() ;
;
(ii)现随机抽取该停车场内停放的3辆车,![]() 表示3辆车中停车费用大于
表示3辆车中停车费用大于![]() 的车辆数,求
的车辆数,求![]() 的概率.
的概率.
参考公式: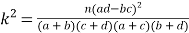 ,其中
,其中![]()
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在区间
,若在区间![]() 内有且只有一个实数
内有且只有一个实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(1)判断函数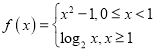 在区间
在区间![]() 内是否具有唯一零点,说明理由:
内是否具有唯一零点,说明理由:
(2)已知向量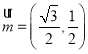 ,
,![]() ,
,![]() ,证明
,证明![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(3)若函数![]() 在区间
在区间![]() 内具有唯一零点,求实数
内具有唯一零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将数列![]() 中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
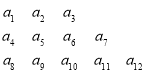
……
记表中的第一列数![]() ,
,![]() ,
,![]() ,…,构成数列
,…,构成数列![]() .
.
(1)设![]() ,求m的值;
,求m的值;
(2)若![]() ,对于任何
,对于任何![]() ,都有
,都有![]() ,且
,且![]() .求数列
.求数列![]() 的通项公式.
的通项公式.
(3)对于(2)中的数列![]() ,若上表中每一行的数按从左到右的顺序均构成公比为q(
,若上表中每一行的数按从左到右的顺序均构成公比为q(![]() )的等比数列,且
)的等比数列,且![]() ,求上表中第k(
,求上表中第k(![]() )行所有项的和
)行所有项的和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年在印度尼西亚日惹举办的亚洲乒乓球锦标赛男子团体决赛中,中国队与韩国队相遇,中国队男子选手A,B,C,D,E依次出场比赛,在以往对战韩国选手的比赛中他们五人获胜的概率分别是0.8,0.8,0.8,0.75,0.7,并且比赛胜负相互独立.赛会釆用5局3胜制,先赢3局者获得胜利.
(1)在决赛中,中国队以3∶1获胜的概率是多少?
(2)求比赛局数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义符号函数![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的最小值.
的最小值.
(2)当![]() 时,函数
时,函数![]() 在
在![]() 上有唯一零点,求
上有唯一零点,求![]() 的取值范围.
的取值范围.
(3)已知存在![]() ,使得
,使得![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com