
【题目】为了美化城市环境,某市针对市民乱扔垃圾现象进行罚款处理。为了更好的了解市民的态度,随机抽取了200人进行了调查,得到如下数据:
罚款金额 | 0 | 5 | 10 | 15 | 20 |
会继续乱扔垃圾的人数 | 80 | 50 | 40 | 20 | 10 |
(1)若乱扔垃圾的人数![]() 与罚款金额
与罚款金额![]() 满足线性回归方程,求回归方程
满足线性回归方程,求回归方程![]() ,其中
,其中![]() ,并据此分析,要使乱扔垃圾者不超过
,并据此分析,要使乱扔垃圾者不超过 ,罚款金额至少是多少元?
,罚款金额至少是多少元?
(2)若以调查数据为基础,从5种罚款金额中随机抽取2种不同的数额,求这两种金额之和不低于25元的概率.
【答案】(1)![]() ,10(2)
,10(2)![]()
【解析】
试题分析:(1)先求出平均值:![]() ,则由
,则由![]() 得
得![]() ,故回归直线方程为
,故回归直线方程为![]() ,由题意列不等式:
,由题意列不等式:![]() 解得
解得![]() (2)利用枚举法得从5种罚款金额中随机抽取2种不同的数额的抽选方法有10种情况,其中两种金额之和不低于25元有4种,再根据古典概型概率求法得概率为:
(2)利用枚举法得从5种罚款金额中随机抽取2种不同的数额的抽选方法有10种情况,其中两种金额之和不低于25元有4种,再根据古典概型概率求法得概率为:![]()
试题解析:(1)由条件可得![]() ,则
,则![]() ,
,
故回归直线方程为![]() ,
,
由![]() 可得
可得![]() ,所以,要使乱扔垃圾者不超过20%,处罚金额至少是10元. (2)设“两种金额之和不低于20元”的事件为A,从5中数额中随机抽取2种,总的抽选方法有(0,5),(0,10),(0,15),(0,20),(5,10),(5,15),(5,20),(10,15),(10,20),(15,20)共10种情况,满足金额之和不低于25元的有4种,故所求概率为:
,所以,要使乱扔垃圾者不超过20%,处罚金额至少是10元. (2)设“两种金额之和不低于20元”的事件为A,从5中数额中随机抽取2种,总的抽选方法有(0,5),(0,10),(0,15),(0,20),(5,10),(5,15),(5,20),(10,15),(10,20),(15,20)共10种情况,满足金额之和不低于25元的有4种,故所求概率为:![]()


科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在如下图象中的两条线段上.该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
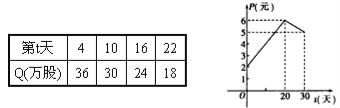
(1)根据提供的图象,写出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.

(1)求证:BC∥DE;
(2)若D、E、C、F四点共圆,且![]() ,求∠BAC.
,求∠BAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列性质,你认为比较恰当的是 ( )
①各棱长相等,同一顶点上的任意两条棱的夹角都相等;
②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;
③各个面都是全等的正三角形,同一顶点上的任意两条棱的夹角都相等.
A. ① B. ③ C. ①② D. .①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点![]() 为中心的
为中心的![]() 海里以内海域被设为警戒水域.点
海里以内海域被设为警戒水域.点![]() 正北
正北![]() 海里有一个雷达观测站
海里有一个雷达观测站![]() ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() ,经过
,经过![]() 分钟又测得该船已行驶到点
分钟又测得该船已行驶到点![]() 北偏东
北偏东![]() (其中
(其中![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() .
.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com