解:(1)因三点M,A
n,B
n共线,
∴

(2分)
得a
n=2+2(n-1)故数列{a
n}的通项公式为a
n=2n(4分)
(2)由题意c
n=8•4
n-3=2
2n-3,

由题意得
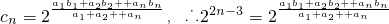
(6分)
∴
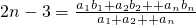
,
∴a
1b
1+a
2b
2+a
nb
n=n(n+1)(2n-3)
当n≥2时,a
nb
n=n(n+1)(2n-3)-(n-1)n(2n-5)=n(6n-8)(8分)
∵a
n=2n
∴b
n=3n-4.
当n=1时,b
1=-1,也适合上式,
∴b
n=3n-4(n∈N
*)(10分)
因为两点P
1、P
n的斜率
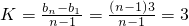
(n∈N
*)为常数
所以点列P
1(1,b
1),P
2(2,b
2),P
n(n,b
n)在同一条直线上.(12分)
(3)由a
n=2n得

;
b
n=3n-4得

(14分)
若a
nB
m=b
nA
m,
则

=4m(m+1-2n)
∵m≥1
∴m=2n-1
∴对任意自然数n,当m=2n-1时,总有a
nB
m=b
nA
m成立.(16分)
分析:(1)由题意知

,由此可得a
n=2+2(n-1),所以数列{a
n}的通项公式为a
n=2n.
(2)由题意得
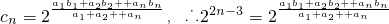
,由此可推导出b
n=3n-4.从而推导出点列P
1(1,b
1),P
2(2,b
2),P
n(n,b
n)在同一条直线上.
(3)由题设条件可知

=4m(m+1-2n),所以对任意自然数n,当m=2n-1时,总有a
nB
m=b
nA
m成立.
点评:本题考查数列性质的综合应用,解题时要认真审题,仔细解答.

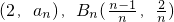 为直角坐标平面上的点.对n∈N*,若三点M,An,B共线,
为直角坐标平面上的点.对n∈N*,若三点M,An,B共线,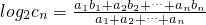 ,其中{cn}是第三项为8,公比为4的等比数列.求证:点列P1(1,b1),P2(2,b2),…Pn(n,bn)在同一条直线上;
,其中{cn}是第三项为8,公比为4的等比数列.求证:点列P1(1,b1),P2(2,b2),…Pn(n,bn)在同一条直线上; (2分)
(2分)
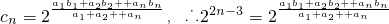 (6分)
(6分)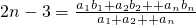 ,
,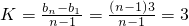 (n∈N*)为常数
(n∈N*)为常数 ;
; (14分)
(14分) =4m(m+1-2n)
=4m(m+1-2n) ,由此可得an=2+2(n-1),所以数列{an}的通项公式为an=2n.
,由此可得an=2+2(n-1),所以数列{an}的通项公式为an=2n.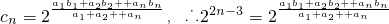 ,由此可推导出bn=3n-4.从而推导出点列P1(1,b1),P2(2,b2),Pn(n,bn)在同一条直线上.
,由此可推导出bn=3n-4.从而推导出点列P1(1,b1),P2(2,b2),Pn(n,bn)在同一条直线上. =4m(m+1-2n),所以对任意自然数n,当m=2n-1时,总有anBm=bnAm成立.
=4m(m+1-2n),所以对任意自然数n,当m=2n-1时,总有anBm=bnAm成立.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案