
某社区举办防控甲型H7N9流感知识有奖问答比赛,甲、乙、丙三人同时回答一道卫生知识题,三人回答正确与错误互不影响。已知甲回答这题正确的概率是 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是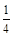 .
.
(I)求乙、丙两人各自回答这道题正确的概率;
(II)用 表示回答该题正确的人数,求
表示回答该题正确的人数,求 的分布列和数学期望
的分布列和数学期望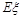 .
.
(Ⅰ)乙回答这题正确的概率是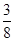 ,丙回答这题正确的概率是
,丙回答这题正确的概率是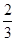 ;
;
(Ⅱ) 的分布列为:
的分布列为: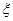
0 1 2 3 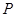
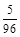
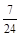
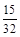
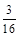
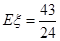 .
.
解析试题分析:(Ⅰ)记“甲、乙、丙回答正确这道题”分别为事件A、B、C,因为甲回答这题正确的概率是 ,
,
所以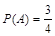 .又甲、丙两人都回答错误的概率是
.又甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是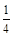 ,由此可得两个方程,即方程组,解这个方程组便可得
,由此可得两个方程,即方程组,解这个方程组便可得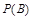 ,
,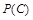 ,即乙、丙两人各自回答这道题正确的概率.
,即乙、丙两人各自回答这道题正确的概率.
(Ⅱ)因为共有3个人,所以回答正确的人数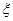 的可能取值为0、1、2、3.由概率公式求出
的可能取值为0、1、2、3.由概率公式求出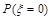 ,
,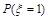 ,
,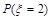 ,
,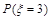 ,便得
,便得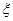 的分布列和期望.
的分布列和期望.
试题解析:(I)记“甲、乙、丙回答正确这道题”分别为事件A、B、C,
则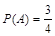 ,且
,且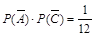 , 1分
, 1分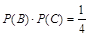 , 2分
, 2分
即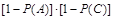 =
= , 3分
, 3分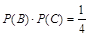 , 4分
, 4分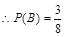 , 5分
, 5分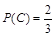 , 6分
, 6分
(II)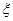 的可能取值为0、1、2、3.
的可能取值为0、1、2、3.
则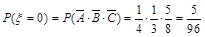 , 7分
, 7分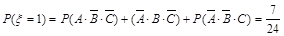 , 8分
, 8分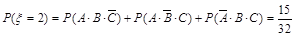 , 9分
, 9分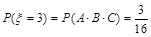 , 10分
, 10分 的分布列为
的分布列为
∴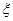
0 1 2 3 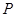
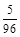
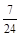
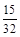
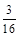
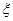 的数学期望
的数学期望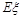 =
=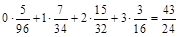 . ………………………………………………12分
. ………………………………………………12分
考点:1、古典概型;2、随机变量的分布列及期望.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为
次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | 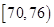 | 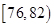 | 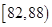 | 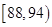 | 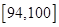 |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司招聘员工采取两次考试(笔试)的方法:第一试考选择题,共10道题(均为四选一题型),每题10分,共100分;第二试考解答题,共3题。规则是:只有在一试中达到或超过80分者才获通过并有资格参加二试,参加二试的人只有答对2题或3题才能被录用。现有甲、乙两人参加该公司的招聘考试。且已知在一试时:两人均会做10道题中的6道;对于另外4道题来说,甲有两题可排除两个错误答案、有两题完全要猜,乙有两题可排除一个错误答案、有一题可排除两个错误答案、有一题完全要猜。进入二试后,对于任意一题,甲答对的概率是 、乙答对的概率是
、乙答对的概率是 .(1)分别求甲、乙两人能通过一试进入二试的概率
.(1)分别求甲、乙两人能通过一试进入二试的概率 、
、 ;(2)求甲、乙两人都能被录用的概率
;(2)求甲、乙两人都能被录用的概率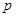 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
)已知某音响设备由五个部件组成,A电视机,B影碟机,C线路,D左声道和E右声道,其中每个部件工作的概率如图所示,能听到声音,当且仅当A与B中有一个工作,C工作,D与E中有一个工作;且若D和E同时工作则有立体声效果.
(1)求能听到立体声效果的概率;
(2)求听不到声音的概率.(结果精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃< t 28℃ 28℃ | 28℃< t  32℃ 32℃ | 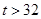 ℃ ℃ |
| 天数 | 6 | 12 |  |  |
 和
和 数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9. ,
, 的值;
的值;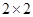 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.| | 高温天气 | 非高温天气 | 合计 |
| 旺销 | 1 | | |
| 不旺销 | | 6 | |
| 合计 | | | |

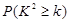 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂三个车间共有工人1000人各车间男、女工人数如表:
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求x的值;
(2)现用分层抽样的方法在第一、第二、第三车间共抽取60名工人参加座谈分,问应在第三车间抽取多少名?
(3)已知y≥185,z≥185,求第三车间中女工比男工少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市 、
、 、
、 、
、 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 |  |  |  |  |
| 人数 |  |  |  |  |
 名参加问卷调查.
名参加问卷调查. 、
、 、
、 、
、 四所中学各抽取多少名学生?
四所中学各抽取多少名学生? 名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率; 名学生中,从来自
名学生中,从来自 、
、 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用 表示抽得
表示抽得 中学的学生人数,求
中学的学生人数,求 的分布列.
的分布列.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名,以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”,求从这16人随机选取3人,至多有1人是“极幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com