
( 10分)如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD= 。
。
1)求证:AO 平面BCD;
平面BCD;
2)求异面直线AB与CD所成角的余弦值;
3)求点E到平面ACD的距离。

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
 11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.查看答案和解析>>
科目:高中数学 来源:2010年吉林省东北师大附中高一下学期期中考试数学 题型:解答题
(本题满分10分)
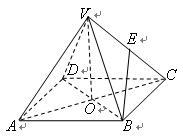
如图,四棱锥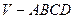 中,底面
中,底面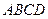 是边长为2的正方形,其余四个侧面都是侧棱长为
是边长为2的正方形,其余四个侧面都是侧棱长为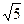 的等腰三角形,且
的等腰三角形,且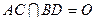 .
.
(1)求证: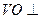 平面
平面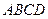 ;
;
(2)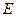 是
是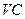 的中点,求
的中点,求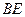 与平面
与平面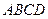 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二下学期期中文科数学试卷(解析版) 题型:解答题
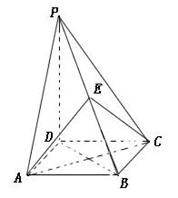
(本小题10分)如图,四棱锥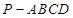 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
(1)求证:平面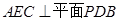 ;
;
(2)当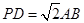 且E为PB的中点时,
求AE与平面PDB所成的角的大小.
且E为PB的中点时,
求AE与平面PDB所成的角的大小.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高二上学期10月月考数学卷 题型:解答题
(本小题满分10分)如图,四棱锥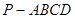 的底面ABCD是正方形,
的底面ABCD是正方形,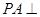 底面ABCD,E,F分别是AC,PB的中点.
底面ABCD,E,F分别是AC,PB的中点.
(I)证明: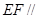 平面PCD;
平面PCD;
(Ⅱ) 若 求EF与平面PAC所成角的大小.
求EF与平面PAC所成角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分10分)如图,四棱锥![]() 的底面是正方形,每条侧棱长都是底面边长的
的底面是正方形,每条侧棱长都是底面边长的![]() 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
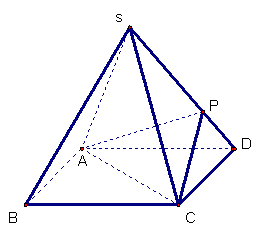 (1)若
(1)若![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(2)在侧棱SC上是否存在一点E,使得![]() ,若存在,求
,若存在,求![]() 的值;若不存在,试说明理由。
的值;若不存在,试说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com