
(00全国卷)(12分)
如图,已知平行六面体ABCD-![]() 的底面ABCD是菱形,且
的底面ABCD是菱形,且![]() =
=
![]()
![]()
(I)证明:![]() ⊥BD;
⊥BD;
(II)当![]() 的值为多少时,能使
的值为多少时,能使![]() 平面
平面![]() ?请给出证明
?请给出证明![]()

解析:(I)证明:连结![]() 、AC,AC和BD交于O,连结
、AC,AC和BD交于O,连结![]()
![]()
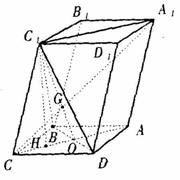
∵ 四边形ABCD是菱形,
∴ AC⊥BD,BC=CD![]()
又∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ DO=OB,
∴ ![]() BD, ――3分
BD, ――3分
但 AC⊥BD,AC∩![]() =O,
=O,
∴ BD⊥平面![]()
![]()
又 ![]() 平面
平面![]() ,
,
∴ ![]() BD
BD![]() ――6分
――6分
(II)当![]() 时,能使
时,能使![]() ⊥平面
⊥平面![]()
![]()
证明一:
∵ ![]() ,
,
∴ BC=CD=![]() ,
,
又 ![]() ,
,
由此可推得BD=![]()
![]()
∴ 三棱锥C- ![]() 是正三棱锥
是正三棱锥![]() ――9分
――9分
设![]() 与
与![]() 相交于G
相交于G![]()
∵ ![]() ∥AC,且
∥AC,且![]() ∶OC=2∶1,
∶OC=2∶1,
∴ ![]() ∶GO=2∶1
∶GO=2∶1![]()
又 ![]() 是正三角形
是正三角形![]() 的BD边上的高和中线,
的BD边上的高和中线,
∴ 点G是正三角形![]() 的中心,
的中心,
∴ CG⊥平面![]()
![]()
即 ![]() ⊥平面
⊥平面![]()
![]() ――12分
――12分
证明二:
由(I)知,BD⊥平面![]() ,
,
∵ ![]()
![]() 平面
平面![]() ,∴ BD⊥
,∴ BD⊥![]()
![]() ――9分
――9分
当 ![]() 时 ,平行六面体的六个面是全等的菱形,
时 ,平行六面体的六个面是全等的菱形,
同BD⊥![]() 的证法可得
的证法可得![]() ⊥
⊥![]()
![]()
又 BD∩![]() =B,
=B,
∴![]() ⊥平面
⊥平面![]()
![]() ――12分
――12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(00全国卷理)(本小题满分14分)
如图,已知梯形ABCD中![]() ,点E分有向线段
,点E分有向线段![]() 所成的比为
所成的比为![]() ,双曲线过C、D、E三点,且以A、B为焦点
,双曲线过C、D、E三点,且以A、B为焦点![]() 当
当![]() 时,求双曲线离心率
时,求双曲线离心率![]() 的取值范围
的取值范围![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
(00全国卷)(12分)
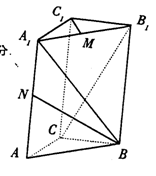
如图,直三棱柱ABC-![]() ,底面ΔABC中,CA=CB=1,BCA=
,底面ΔABC中,CA=CB=1,BCA=![]() ,棱
,棱![]() =2,M、N分别是
=2,M、N分别是![]() 、
、![]() 的中点
的中点![]()
(I)求![]() 的长;
的长;
(II)求![]() ,
,![]()
![]() 的值;
的值;
(III)求证![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com