
某地有10个著名景点,其中8 个为日游景点,2个为夜游景点.某旅行团要从这10个景点中选5个作为二日游的旅游地.行程安排为第一天上午、下午、晚上各一个景点,第二天上午、下午各一个景点.
(1)甲、乙两个日游景点至少选1个的不同排法有多少种?
(2)甲、乙两日游景点在同一天游玩的不同排法有多少种?
(3)甲、乙两日游景点不同时被选,共有多少种不同排法?
(1)甲、乙两个日游景点至少选1个的不同排法有2640种;
(2)甲、乙两日游景点在同一天游玩的不同排法有240种;
(3)甲、乙两日游景点不同时被选,共有2640种不同排法.
解析试题分析:(1)甲、乙两个日游景点选1个为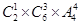 种,甲、乙两个日游景点都选有
种,甲、乙两个日游景点都选有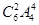 ,夜游景点的选法为
,夜游景点的选法为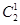 种,所以有
种,所以有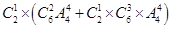 种;
种;
(2)甲、乙两日游景点在同一天游玩:排在第一天或第二天有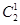 种,安排在上下午有
种,安排在上下午有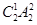 种,剩下的两个景点从除去甲乙外的6个里选有
种,剩下的两个景点从除去甲乙外的6个里选有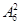 种,共
种,共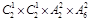 种;
种;
(3)日游景点的排法为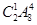 种,甲、乙两日游景点都不选有
种,甲、乙两日游景点都不选有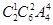 种,所以甲、乙两日游景点不同时被选,共有
种,所以甲、乙两日游景点不同时被选,共有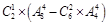 种不同排法.
种不同排法.
(1)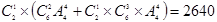 (种) 5分
(种) 5分
(2)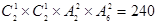 (种) 10分
(种) 10分
(3)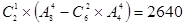 (种) 15分
(种) 15分
答:分别不同排法总数是2640种,240种,2640种. 16分
考点:排列组合综合应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(14分)已知在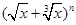 (其中n<15)的展开式中:
(其中n<15)的展开式中:
(1)求二项式展开式中各项系数之和;
(2)若展开式中第9项,第10项,第11项的二项式系数成等差数列,求n的值;
(3)在(2)的条件下写出它展开式中的有理项.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数:
(1)选其中5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站在排头也不站在排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻;
(6)全体排成一排,甲、乙两人中间恰好有3人.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由数字1、2、3、4、5、6组成无重复数字的数中,求:
(1)六位偶数的个数;
(2)求三个偶数互不相邻的六位数的个数;
(3)求恰有两个偶数相邻的六位数的个数;
(4)奇数字从左到右,从小到大依次排列的六位数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•浙江)设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和.,求ξ分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若 ,求a:b:c.
,求a:b:c.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知10件不同产品中共有4件次品,现对它们进行一一测试,直至找到所有次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品的不同测试方法数有多少种?
(2)若恰在第5次测试后,就找出了所有次品,则这样的不同测试方法数有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com