
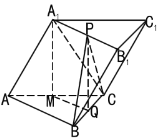
【题目】已知斜三棱柱![]() 的侧面
的侧面![]() 与底面
与底面![]() 垂直,
垂直,![]() ,
,![]() ,且
,且![]() ,
,![]() ,求:
,求:
(1)侧棱![]() 与底面
与底面![]() 所成角的大小;
所成角的大小;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.

【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由已知得直线![]() 在底面
在底面![]() 内的射影为直线
内的射影为直线![]() ,得
,得![]() 为侧棱
为侧棱![]() 与底面
与底面![]() 所成的角,由此能求出侧棱
所成的角,由此能求出侧棱![]() 与底面
与底面![]() 所成角的大小.
所成角的大小.
(2)求点![]() 到平面
到平面![]() 的距离也是求点
的距离也是求点![]() 到平面
到平面![]() 的距离,再用等体积法
的距离,再用等体积法![]() ,求出三棱锥
,求出三棱锥![]() 的高就是求出点
的高就是求出点![]() 到平面
到平面![]() 的距离.
的距离.
解:(1)取![]() 中点
中点![]() ,连接
,连接![]()
∵平面![]()
![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,
,
又因为![]() ,所以
,所以![]() 又
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 为
为![]() 在平面
在平面![]() 上的射影,所以
上的射影,所以![]() 为
为![]() 与平面
与平面![]() 所成的角
所成的角
∵![]() 且
且![]() ,∴
,∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]()
所以![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 。
。
(2)取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连接
,连接![]()
∵![]() ∴
∴![]() 平面
平面![]() ∴
∴![]() 且
且![]()
∴![]() 平面
平面![]() ∴
∴![]() ∴
∴![]()
在直角三角形![]() 中,由
中,由![]() ,得
,得![]()
∴![]() ∴
∴![]()
设点![]() 到平面
到平面![]() 得距离为
得距离为![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 到平面
到平面![]() 得距离与
得距离与![]() 到平面
到平面![]() 的距离相等,
的距离相等,
∵![]() 平面
平面![]() ∴
∴![]() 平面
平面![]() ∴
∴![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由![]() ,得
,得![]() ……①
……①
而![]() ,
,![]() ,
,![]()
将数据代入①式得![]() ,
,![]() ,
,
即![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
故得解.


科目:高中数学 来源: 题型:
【题目】如图(示意),公路AM、AN围成的是一块顶角为钝角α的角形耕地,其中![]() .在该块土地中
.在该块土地中![]() 处有一小型建筑,经测量,它到公路
处有一小型建筑,经测量,它到公路![]() 、
、![]() 的距离
的距离![]() 、
、![]() 分别为
分别为![]() ,
,![]() .现要过点
.现要过点![]() 修建一条直线公路
修建一条直线公路![]() ,将三条公路围成的区域
,将三条公路围成的区域![]() 建成一个工业园.设
建成一个工业园.设![]() ,
,![]()
![]() ,其中
,其中![]() .
.

(1)试建立![]() 间的等量关系;
间的等量关系;
(2)为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民营企业生产A,B两种产品,根据市场调查与预测,A产品的利润y与投资x成正比,其关系如图甲,B产品的利润y与投资x的算术平方根成正比,其关系如图乙![]() 注:利润与投资单位为万元
注:利润与投资单位为万元![]()
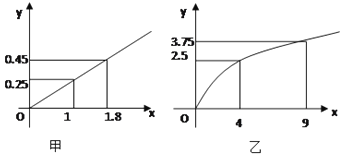
![]() 分别将A,B两种产品的利润y表示为投资x的函数关系式;
分别将A,B两种产品的利润y表示为投资x的函数关系式;
![]() 该企业已筹集到10万元资金,并全部投入A,B两种产品的生产
该企业已筹集到10万元资金,并全部投入A,B两种产品的生产![]() 问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汕头某家电企业要将刚刚生产的100台变频空调送往市内某商场,现有4辆甲型货车和8辆乙型货车可供调配,每辆甲型货车的运输费用是400元,可装空调20台,每辆乙型货车的运输费用是300元,可装空调10台,若每辆车至多运一次,则企业所花的最少运费为( )
A. 2000元B. 2200元C. 2400元D. 2800元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() ,
,
(1) 判断![]() 的奇偶性并证明;
的奇偶性并证明;
(2) 令![]()
①判断![]() 在
在![]() 的单调性(不必说明理由);
的单调性(不必说明理由);
②是否存在![]() ,使得
,使得![]() 在区间
在区间![]() 的值域为
的值域为![]() ?若存在,求出此时
?若存在,求出此时![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com