Question

【题目】已知抛物线的焦点为，过点的直线与相交于两点，点关于轴的对称点为.

（Ⅰ）证明：点在直线上；

（Ⅱ）设，求的内切圆的方程.

Answer 1

【答案】(Ⅰ)证明见解析；

(Ⅱ) .

【解析】试题分析：（Ⅰ）先根据抛物线方程求得焦点坐标，设出过点的直线方程代入抛物线方程消去，设与 的交点， ，根据韦达定理求得和的表达式，进而根据点求得点的坐标，进而表示出直线的直线方程，求出直线在轴上的截距进而原式得证；（Ⅱ）首先表示出结果为求得，进而求得的值，推知的斜率，则方程可知，设，利用点到直线的距离进而求得和圆的半径，则圆的方程可得．

试题解析：（Ⅰ）设， ， ，

的方程为.

将代入得到：

由韦达定理知道：

所以直线BD 的方程为： ，

即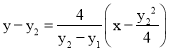

令得到： =1

所以点F（1,0）在直线BD上

（Ⅱ）由①知，

因为 ，

故， 解得

所以的方程为

又由①知 ，故直线BD的斜率，

因而直线BD的方程为

因为KF为的平分线，故可设圆心，

到及BD的距离分别为.

由得，或（舍去），

故圆M的半径.

所以圆M的方程为.