练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知正四棱锥O-ABCD的体积为
    3
    		2
    2
    ，底面边长为
    		3
    ，则以O为球心，OA为半径的球的表面积为
    24π
    24π
    ．
    分析：先直接利用锥体的体积公式即可求得正四棱锥O-ABCD的高，再利用直角三角形求出正四棱锥O-ABCD的侧棱长OA，最后根据球的表面积公式计算即得．
    解答：解：如图，正四棱锥O-ABCD的体积V=
    1
    3
    sh=
    1
    3
    （
    		3
    ×
    		3
    ）×OH=
    3
    		2
    2
    ，
    ∴OH=
    3
    		2
    2
    ，
    在直角三角形OAH中，OA=
    		AH2+OH2
    =
    		(
    3
    		2
    2
    )    2    +(
    		6
    2
    )    2
    =
    		6

    所以表面积为4πr2=24π；
    故答案为：24π．
    点评：本题考查锥体的体积、球的表面积计算，考查学生的运算能力，属基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知正四棱柱ABCD-A1B1C1D1的底面边长AB=6，侧棱长AA1=2
    		7
    ，它的外接球的球心为O，
    点E是AB的中点，点P是球O的球面上任意一点，有以下判断：
    （1）PE长的最大值是9；
    （2）P到平面EBC的距离最大值是4+
    		7
    ；
    （3）存在过点E的平面截球O的截面面积是3π；
    （4）三棱锥P-AEC1体积的最大值是20．
    其中正确判断的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知正四棱柱ABCD-A1B1C1D1的底面边长AB=6，侧棱长AA1=2
    		7
    ，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，有以下判断，
    （1）PE长的最大值是9；（2）三棱锥P-EBC的最大值是
    32
    3
    ；（3）存在过点E的平面，截球O的截面面积是3π；（4）三棱锥P-AEC1体积的最大值是20．
    正确的是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　人教课标高一版(A必修2)　2009－2010学年　第23期　总179期 人教课标高一版 题型：044

    已知正四棱锥V－ABCD中，O为底面中心，|AB|＝2，|VO|＝3，以O为坐标原点，射线OA为x轴，射线OB为y轴，射线OV为z轴，建立如图所示的空间直角坐标系Oxyz，试确定各顶点的坐标．

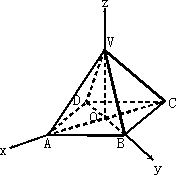
    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年四川宜宾市高三第一次诊断性考试文科数学试卷（解析版） 题型：填空题

    已知正四棱柱ABCD—A1B1C1D1的底面边长AB=6，侧棱长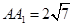，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，则有以下结论：

    ①PE长的最大值是9；

    ②三棱锥P—EBC的最大值是[]

    ③存在过点E的平面，截球O的截面面积是；

    ④三棱锥P—AEC1体积的最大值是20。

    其中正确结论的是           。（写出所有正确结论的序号）

     

    查看答案和解析>>

    科目：高中数学 来源：2010年河南省豫南九校高考数学仿真模拟试卷（理科）（解析版） 题型：解答题

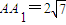    已知正四棱柱ABCD-A1B1C1D1的底面边长AB=6，侧棱长，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，有以下判断，
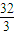    （1）PE长的最大值是9；（2）三棱锥P-EBC的最大值是；（3）存在过点E的平面，截球O的截面面积是3π；（4）三棱锥P-AEC1体积的最大值是20．
    正确的是    ．

    查看答案和解析>>

    同步练习册答案