练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】各项均为正数的等差数列{an}前n项和为Sn ， 首项a1=3，数列{bn} 为等比数列，首项b1=1，且b2S2=64，b3S3=960．
    （1）求an和bn；
    （2）设f（n）= （n∈N*），求f（n）最大值及相应的n的值．

    【答案】
    （1）解：设等差数列{an}的公差为d，等比数列{bn}的公比为q，则d＞0，

    ∴ ，

    依题意： ，解得 或 （舍）．

    ∴an=2n+1， ；


    （2）解：∵Sn=n（n+2），

    ∴f（n）= = ≤ ．

    当且仅当n= ，即n=10时取等号．

    ∴当n=10时，所求最小值为


    【解析】（1）设出等差数列的公差和等比数列的公比，由已知列式求得等差数列的公差和等比数列的公比，则an和bn可求；（2）把等差数列{an}的通项和前n项和为Sn代入f（n）= ，整理后利用基本不等式求得f（n）最大值及相应的n的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，棱柱ABCD﹣A1B1C1D1的底面是菱形．侧棱长为5，平面ABCD⊥平面A1ACC1 ， AB=3 ，∠BAD=60°，点E是△ABD的重心，且A1E=4．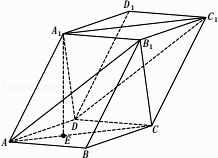
    （1）求证：平面A1DC1∥平面AB1C；
    （2）求二面角B1﹣AC﹣B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱ABC﹣A1B1C1中，侧棱与底面垂直，AB=AC=1，AA1=2，且P，Q，M分别是BB1 ， CC1 ， B1C1的中点，AB⊥AQ．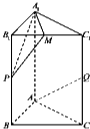

    （1）求证：AB⊥AC；
    （2）求证：AQ∥平面A1PM；
    （3）求AQ与平面BCC1B1所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}中，a1=3，n（an+1﹣an）=an+1，n∈N*若对于任意的a∈[﹣1，1]，n∈N* ， 不等式 ﹣2at+1恒成立，则实数t的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷水的高度，某人在喷水柱正西方向的点A测的水柱顶端的仰角为45°，沿点A向北偏东30°前进100m到达点B．在B点测得水柱顶端的仰角为30°，则水柱的高度是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}中，a1=3，a2=5，其前n项和为Sn满足Sn+Sn﹣2=2Sn﹣1+2n﹣1（n≥3，n∈N*）
    （1）试求数列{an}的通项公式
    （2）令bn= ，Tn是数列{bn}的前n项和．证明：对任意给定的m∈（0， ），均存在n0∈N*，使得当n≥n0时，Tn＞m恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】钝角△OAB三边的比为2 ：2 ：（ ﹣ ），O为坐标原点，A（2，2 ）、B（a，a），则a的值为（ ）
    A.2
    B.
    C.2 或
    D. +

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在圆内接△ABC，A，B，C所对的边分别为a，b，c，满足acosC+ccosA=2bcosB．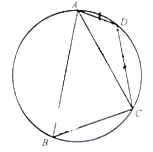
    （1）求B的大小；
    （2）若点D是劣弧 上一点，AB=3，BC=2，AD=1，求四边形ABCD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（﹣2，1）， =（3，﹣4）．
    （1）求（ + ）（2 ﹣ ）的值；
    （2）求向量 与 + 的夹角．

    查看答案和解析>>

    同步练习册答案