
分析 (Ⅰ)由题意可知n,$\overline{x}$,$\overline{y}$,进而代入可得b、a值,可得方程;
(Ⅱ)由回归方程x的系数b的正负可判断;
(Ⅲ)把x=7代入回归方程求其函数值即可.
解答 解:(Ⅰ)由题意知,n=10,$\overline{x}$=8,$\overline{y}$=2,
∴b=$\frac{184-10×8×2}{720-10×{8}^{2}}$=0.3,a=2-0.3×8=-0.4,
∴y=0.3x-0.4.…(4分)
(Ⅱ)由于b=0.3>0,
∴y与x之间是正相关.…(6分)
(Ⅲ))x=7时,y=0.3×7-0.4=1.7(千元).…(8分)
点评 本题考查线性回归方程的求解及应用,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{27\sqrt{3}}{2}$ | B. | $\frac{27\sqrt{35}}{2}$ | C. | $\frac{27}{2}$($\sqrt{3}$+$\sqrt{35}$) | D. | $\frac{27}{2}$($\sqrt{35}$-$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {x|-1≤x≤0} | C. | {x|1≤x≤2} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
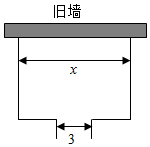 如图所示,要围建一个面积为400m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙时需要维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为3m的进出口,已知旧墙的维修费用为56元/m,新墙的造价为200元/m,设利用旧墙的长度为x(单位:m),修建此矩形场地的总费用为y(单位:元).
如图所示,要围建一个面积为400m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙时需要维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为3m的进出口,已知旧墙的维修费用为56元/m,新墙的造价为200元/m,设利用旧墙的长度为x(单位:m),修建此矩形场地的总费用为y(单位:元).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com