
【题目】设![]() ,若
,若![]() ,求证:
,求证:
(1)方程![]() 有实根.
有实根.
(2)若﹣2<![]() <﹣1且设x1,x2是方程f(x)=0的两个实根,则
<﹣1且设x1,x2是方程f(x)=0的两个实根,则![]() ≤|x1﹣x2|<
≤|x1﹣x2|<![]()
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(Ⅰ)针对a进行分类讨论,当a=0时,f(0)f(1)≤0显然与条件矛盾,当a≠0时,f(x)=3ax2+2bx+c为二次函数,只需考虑判别式大于等于零即可;
(Ⅱ)利用根与系数的关系将(x1﹣x2)2转化成关于![]() 的二次函数,根据
的二次函数,根据![]() 的范围求出值域即可.
的范围求出值域即可.
试题解析:
证明:(1)若a=0,则b=﹣c,
f(0)f(1)=c(3a+2b+c)=﹣c2≤0,
与已知矛盾,所以a≠0.
方程3ax2+2bx+c=0的判别式△=4(b2﹣3ac),
由条件a+b+c=0,消去b,得△=4(a2+c2﹣ac)=![]()
故方程f(x)=0有实根.
(2)由条件,知![]() ,
,![]() ,
,
所以(x1﹣x2)2=(x1+x2)2﹣4x1x2=![]() .
.
因为﹣2<![]() <﹣1所以
<﹣1所以![]()
故![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
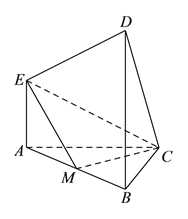
【题目】在如图所示的多面体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .若存在,指出点
.若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数,
为参数, ![]() ).
).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站针对2015年中国好声音歌手A,B,C三人进行网上投票,结果如下
观众年龄 | 支持A | 支持B | 支持C |
20岁以下 | 100 | 200 | 600 |
20岁以上(含20岁) | 100 | 100 | 400 |
(1)在所有参与该活动的人中,用分层抽样的方法抽取n人,其中有6人支持A,求n的值.
(2)在支持C的人中,用分层抽样的方法抽取5人作为一个总体,从这5人中任意选取2人,求恰有1人在20岁以下的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解今年高中毕业生的体能状况,从某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.数据分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 .第6小组的频数是7.
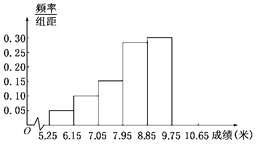
(I)求这次铅球测试成绩合格的人数;
(II)若参加测试的学生中9人成绩优秀,现要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知学生![]() 、
、![]() 的成绩均为优秀,求两人
的成绩均为优秀,求两人![]() 、
、![]() 至少有1人入选的概率.
至少有1人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知四棱锥P﹣ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证: 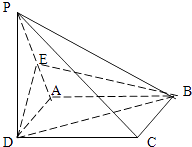
(1)PC∥平面EBD.
(2)平面PBC⊥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com