
【题目】已知函数![]() 是奇函数,且
是奇函数,且![]() =10
=10
(1)求![]() 的解析式;
的解析式;
(2)判断函数![]() 在
在![]() 上的单调性,并加以证明.
上的单调性,并加以证明.
(3)函数![]() 在[-3,0)上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
在[-3,0)上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义域为
是定义域为![]() 上的函数,若对任意的实数
上的函数,若对任意的实数![]() ,都有:
,都有:![]() 成立,当且仅当
成立,当且仅当![]() 时取等号,则称函数
时取等号,则称函数![]() 是
是![]() 上的凸函数,凸函数具有以下性质:对任意的实数
上的凸函数,凸函数具有以下性质:对任意的实数![]() ,都有:
,都有:![]() 成立,当且仅当
成立,当且仅当![]() 时取等号,设
时取等号,设![]()
(1)求证:![]() 是
是![]() 上的凸函数
上的凸函数
(2)设![]() ,
,![]() ,利用凸函数的定义求
,利用凸函数的定义求![]() 的最大值
的最大值
(3)设![]() 是
是![]() 三个内角,利用凸函数性质证明
三个内角,利用凸函数性质证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台为宣传本省,随机对本省内![]() 岁的人群抽取了n人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示
岁的人群抽取了n人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示
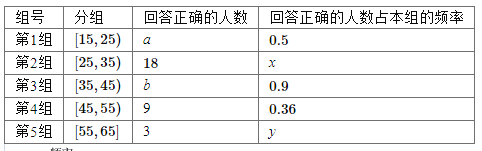
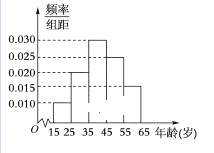
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取6人,求第
组回答正确的人中用分层抽样的方法抽取6人,求第![]() 组每组各抽取多少人?
组每组各抽取多少人?
(3)指出直方图中,这组数据的中位数是多少(取整数值)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是AA1,D1C1的中点,过D,M,N三点的平面与正方体的下底面A1B1C1D1相交于直线l.

(1)画出直线l的位置,并简单指出作图依据;
(2)设l∩A1B1=P,求线段PB1的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为15000元.旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数不超过35人时,飞机票每张收费800元;若旅游团的人数多于35人,则给予优惠,每多1人,机票费每张减少10元,但旅游团的人数最多有60人.设旅行团的人数为![]() 人,飞机票价格为
人,飞机票价格为![]() 元,旅行社的利润为
元,旅行社的利润为![]() 元.
元.
(1)写出飞机票价格![]() 元与旅行团人数
元与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当旅游团的人数![]() 为多少时,旅行社可获得最大利润?求出最大利润.
为多少时,旅行社可获得最大利润?求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其它各面用钢筋网围成.
(1)现有可围![]() 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
(2)若使每间虎笼面积为![]() ,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?
,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com