
【题目】对于无穷数列![]() ,“若存在
,“若存在![]() ,必有
,必有![]() ”,则称数列
”,则称数列![]() 具有
具有![]() 性质.
性质.
(1)若数列![]() 满足
满足 ,判断数列
,判断数列![]() 是否具有
是否具有![]() 性质?是否具有
性质?是否具有![]() 性质?
性质?
(2)对于无穷数列![]() ,设
,设![]() ,求证:若数列
,求证:若数列![]() 具有
具有![]() 性质,则
性质,则![]() 必为有限集;
必为有限集;
(3)已知![]() 是各项均为正整数的数列,且
是各项均为正整数的数列,且![]() 既具有
既具有![]() 性质,又具有
性质,又具有![]() 性质,是否存在正整数
性质,是否存在正整数![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…成等差数列.若存在,请加以证明;若不存在,说明理由.
,…成等差数列.若存在,请加以证明;若不存在,说明理由.
【答案】(1)见解析;
(2)见解析;
(3)见解析.
【解析】
(1)根据题中所给的条件,利用定义判断可得数列![]() 不具有性质
不具有性质![]() ,具有性质
,具有性质![]() ;
;
(2)根据数列具有性质![]() ,得到数列
,得到数列![]() 元素个数,从而证得结果;
元素个数,从而证得结果;
(3)依题意,数列![]() 是各项为正数的数列,且
是各项为正数的数列,且![]() 既具有
既具有![]() 性质,又具有
性质,又具有![]() 性质,可证得存在整数
性质,可证得存在整数![]() ,使得
,使得![]() 是等差数列.
是等差数列.
(1)因为 ,
,
![]() ,但
,但![]() ,所以数列
,所以数列![]() 不具有性质
不具有性质![]() ,
,
同理可得数列![]() 具有性质
具有性质![]() ;
;
(2)因为数列![]() 具有性质
具有性质![]() ,
,
所以一定存在一组最小的且![]() ,满足
,满足![]() ,即
,即![]() ,
,
由性质![]() 的含义可得
的含义可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以数列![]() 中,从第
中,从第![]() 项开始的各项呈现周期性规律:
项开始的各项呈现周期性规律:
![]() 为一个周期中的各项,
为一个周期中的各项,
所以数列![]() 中最多有
中最多有![]() 个不同的项,
个不同的项,
所以![]() 最多有
最多有![]() 个元素,即
个元素,即![]() 为有限集;
为有限集;
(3)因为数列![]() 具有
具有![]() 性质,又具有
性质,又具有![]() 性质,
性质,
所以存在![]() ,使得
,使得![]() ,
,
其中![]() 分别是满足上述关系式的最小的正整数,
分别是满足上述关系式的最小的正整数,
由性质![]() 的含义可得
的含义可得![]() ,
,
若![]() ,则取
,则取![]() ,可得
,可得![]() ,
,
若![]() ,则取
,则取![]() ,可得
,可得![]() ,
,
记![]() ,则对于
,则对于![]() ,
,
有![]() ,显然
,显然![]() ,
,
由性质![]() 的含义可得:
的含义可得:![]() ,
,
所以![]()
![]() ,
,
所以![]() ,
,
又![]() 满足
满足![]() 的最小的正整数,
的最小的正整数,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
取![]() ,所以,若
,所以,若![]() 是偶数,则
是偶数,则![]() ,
,
若![]() 是奇数,
是奇数,
则![]() ,
,
所以,![]() ,
,
所以![]() 是公差为1的等差数列.
是公差为1的等差数列.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省高考改革实施方案指出:该省高考考生总成绩将由语文、数学、外语3门统一高考成绩和学生自主选择的学业水平等级性考试科目共同构成.该省教育厅为了解正就读高中的学生家长对高考改革方案所持的赞成态度,随机从中抽取了100名城乡家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见.下面是根据样本的调查结果绘制的等高条形图.
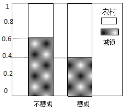
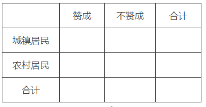
(1)根据已知条件与等高条形图完成下面的2×2列联表,并判断我们能否有95%的把握认为“赞成高考改革方案与城乡户口有关”?
(2)利用分层抽样从持“不赞成”意见家长中抽取5名参加学校交流活动,从中选派2名家长发言,求恰好有1名城镇居民的概率.
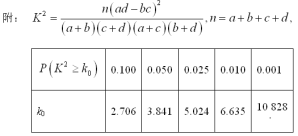
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国国际智能产业博览会(智博会)每年在重庆市举办一届,每年参加服务的志愿者分“嘉宾”、“法医”等若干小组![]() 年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出50人作为2019年中国国际智博会服务的志愿者.
年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出50人作为2019年中国国际智博会服务的志愿者.
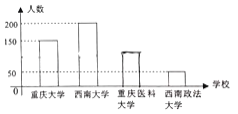
(1)若“嘉宾”小组需要2名志愿者,求这2人分别来自不同大学的概率(结果用分数表示)
(2)若“法医”小组的3名志愿者只能从重庆医科大学或西南政法大学抽出,用![]() 表示抽出志愿者来自重庆医科大学的人数,求
表示抽出志愿者来自重庆医科大学的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为实常数,函数
为实常数,函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() ,不等式
,不等式![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() ,当
,当![]() 时,是否存在正整数
时,是否存在正整数![]() ,使得
,使得![]() 或
或![]() 成立.若存在,试找出所有的m;若不存在,请说明理由.
成立.若存在,试找出所有的m;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四人进行一项益智游戏,方法如下:第一步:先由四人看着平面直角坐标系中方格内的16个棋子(如图所示),甲从中记下某个棋子的坐标;第二步:甲分别告诉其他三人:告诉乙棋子的横坐标.告诉丙棋子的纵坐标,告诉丁棋子的横坐标与纵坐标相等;第三步:由乙、丙、丁依次回答.对话如下:“乙先说我无法确定.丙接着说我也无法确定.最后丁说我知道”.则甲记下的棋子的坐标为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com