
【题目】已知圆C:x2+y2﹣2x+4my+4m2=0,圆C1:x2+y2=25,以及直线l:3x﹣4y﹣15=0.
(1)求圆C1:x2+y2=25被直线l截得的弦长;
(2)当m为何值时,圆C与圆C1的公共弦平行于直线l;
(3)是否存在m,使得圆C被直线l所截的弦AB中点到点P(2,0)距离等于弦AB长度的一半?若存在,求圆C的方程;若不存在,请说明理由.
【答案】解:(1)因为圆![]() 的圆心O(0,0),半径r=5,
的圆心O(0,0),半径r=5,
所以,圆心O到直线l:3x﹣4y﹣15=0的距离d:![]() ,由勾股定理可知,
,由勾股定理可知,
圆![]() 被直线l截得的弦长为
被直线l截得的弦长为![]() .
.
(2)圆C与圆C1的公共弦方程为2x﹣4my﹣4m2﹣25=0,
因为该公共弦平行于直线3x﹣4y﹣15=0,
则![]() ≠
≠![]() ,
,
解得:m=![]()
经检验m=![]() 符合题意,故所求m=
符合题意,故所求m=![]() ;
;
(3)假设这样实数m存在.
设弦AB中点为M,由已知得|AB|=2|PM|,即|AM|=|BM|=|PM|
所以点P(2,0)在以弦AB为直径的圆上.
设以弦AB为直径的圆方程为:x2+y2﹣2x+4my+4m2+λ(3x﹣4y﹣15)=0,
则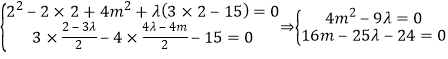
消去λ得:100m2﹣144m+216=0,25m2﹣36m+54=0
因为△=362﹣4×25×54=36(36﹣25×6)<0
所以方程25m2﹣36m+54=0无实数根,
所以,假设不成立,即这样的圆不存在.
【解析】(1)根据直线和圆相交的弦长公式即可求圆C1:x2+y2=25被直线l截得的弦长;
(2)求出两圆的公共弦结合直线平行的条件即可求出直线l;
(3)根据两点间的距离公式结合弦长关系即可得到结论.


科目:高中数学 来源: 题型:
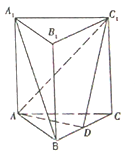
【题目】如图,三棱柱![]() 中,底面
中,底面![]() 为正三角形,
为正三角形, ![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在侧棱![]() 上是否存在一点
上是否存在一点![]() ,使得三棱锥
,使得三棱锥![]() 的体积是
的体积是![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一条生产线上按同样的方式每隔30分钟取一件产品,共取了n件,测得其产品尺寸后,画得其频率分布直方图如图所示,已知尺寸在[15,45)内的频数为46. 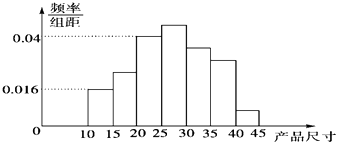
(1)该抽样方法是什么方法?
(2)求n的值;
(3)求尺寸在[20,25)内的产品的件数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车的计价标准是:4km以内(含4km)10元,超过4km且不超过18km的部分1.2元/km,超过18km的部分1.8元/km,不计等待时间的费用.
(1)如果某人乘车行驶了10km,他要付多少车费?
(2)试建立车费y(元)与行车里程x(km)的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),
),![]() 为
为![]() 上一点,以
上一点,以![]() 为边作等边三角形
为边作等边三角形![]() ,且
,且![]() 、
、![]() 、
、![]() 三点按逆时针方向排列.
三点按逆时针方向排列.
(Ⅰ)当点![]() 在
在![]() 上运动时,求点
上运动时,求点![]() 运动轨迹的直角坐标方程;
运动轨迹的直角坐标方程;
(Ⅱ)若曲线![]() :
: ![]() ,经过伸缩变换
,经过伸缩变换![]() 得到曲线
得到曲线![]() ,试判断点
,试判断点![]() 的轨迹与曲线
的轨迹与曲线![]() 是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
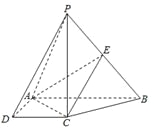
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com