
【题目】如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C: ![]() 经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
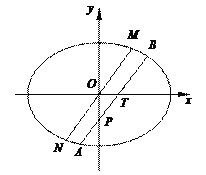
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求 ![]() 的值;
的值;
(3)记直线l与y轴的交点为P.若![]() ,求直线l的斜率k.
,求直线l的斜率k.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据题意,把点代入椭圆的方程和![]() ,列出方程组,求解
,列出方程组,求解![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立方程组,利用根与系数的关系,写出韦达定理,又由
,联立方程组,利用根与系数的关系,写出韦达定理,又由![]() ,得
,得![]() 的方程为
的方程为![]() ,联立方程组,求得点
,联立方程组,求得点![]() 的坐标,即可求解结论;
的坐标,即可求解结论;
(3)由直线![]() ,得
,得![]() ,求得
,求得![]() 的坐标,再根据
的坐标,再根据![]() ,得到
,得到![]() ,由(2)中的韦达定理,得出关于
,由(2)中的韦达定理,得出关于![]() 的方程,即可求解结论。
的方程,即可求解结论。
试题解析:
(1)因为椭圆![]() +
+![]() =1经过点(b,2e),所以
=1经过点(b,2e),所以![]() +
+![]() =1.
=1.
因为e2=![]() =
=![]() ,所以
,所以![]() +
+![]() 1.
1.
因为a2=b2+c2,所以![]() +
+![]() =1.
=1.
整理得 b4-12b2+32=0,解得b2=4或b2=8(舍) .
所以椭圆C的方程为![]() +
+![]() =1.
=1.
(2)设A(x1,y1),B(x2,y2).因为T(1,0),则直线l的方程为y=k(x-1).
联立直线l与椭圆方程 ![]()
消去y,得 (2k2+1)x2-4k2x+2k2-8=0,
所以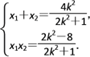
因为MN∥l,所以直线MN方程为y=kx,
联立直线MN与椭圆方程![]()
消去y得 (2k2+1)x2=8,解得x2=![]() .
.
因为MN∥l,所以![]() =
=![]() .
.
因为 (1-x1)·(x2-1)=-[x1x2-(x1+x2)+1]=![]() ,
,
(xM-xN)2=4x2=![]() ,
,
所以![]() =
=![]() =
=![]() ·
·![]() =
=![]() .
.
(3)在y=k(x-1)中,令x=0,则y=-k,所以P(0,-k),
从而![]() =(-x1,-k-y1),
=(-x1,-k-y1),![]() =(x2-1,/span>y2).
=(x2-1,/span>y2).
因为![]() =
=![]() ,所以-x1= (x2-1),即x1+x2=.由(2)知,
,所以-x1= (x2-1),即x1+x2=.由(2)知, 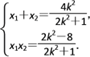
由 解得 x1=
解得 x1=![]() ,x2=
,x2=![]() .因为x1x2=
.因为x1x2=![]() , 所以
, 所以![]() ×
×![]() =
=![]() ,
,
整理得 50k4-83k2-34=0,解得k2=2或k2=-![]() (舍) .
(舍) .
又因为k>0,所以k=![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为D,若对于任意x1、x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x+sinπx﹣3的某一个对称中心,并利用对称中心的上述定义,可得到f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )的值为( )
)的值为( )
A.4027
B.﹣4027
C.8054
D.﹣8054
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,如果存在区间
,如果存在区间![]() (
(![]() ),同时满足:
),同时满足:
①![]() 在
在![]() 内是单调函数;②当定义域是
内是单调函数;②当定义域是![]() 时,
时, ![]() 的值域也是
的值域也是![]() .
.
则称函数![]() 是区间
是区间![]() 上的“保值函数”.
上的“保值函数”.
(1)求证:函数![]() 不是定义域
不是定义域![]() 上的“保值函数”;
上的“保值函数”;
(2)已知![]() (
(![]() )是区间
)是区间![]() 上的“保值函数”,求
上的“保值函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
A.选修4—1:几何证明选讲
如图,△ABC的顶点A,C在圆O上,B在圆外,线段AB与圆O交于点M.

(1)若BC是圆O的切线,且AB=8,BC=4,求线段AM的长度;
(2)若线段BC与圆O交于另一点N,且AB=2AC,求证:BN=2MN.
B.选修4—2:矩阵与变换
设a,b∈R.若直线l:ax+y-7=0在矩阵A= ![]() 对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
对应的变换作用下,得到的直线为l′:9x+y-91=0.求实数a,b的值.
C.选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,直线l:  (t为参数),与曲线C:
(t为参数),与曲线C:  (k为参数)交于A,B两点,求线段AB的长.
(k为参数)交于A,B两点,求线段AB的长.
D.选修4—5:不等式选讲
设a≠b,求证:a4+6a2b2+b4>4ab(a2+b2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣1(x≥0)的图象经过点(2, ![]() ),其中a>0,a≠1.
),其中a>0,a≠1.
(1)求a的值;
(2)求函数f(x)=a2x﹣ax﹣2+8,x∈[﹣2,1]的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生产甲乙两种精密电子产品,用以下两种方案分别生产出甲乙产品共![]() 种,现对这两种方案生产的产品分别随机调查了各
种,现对这两种方案生产的产品分别随机调查了各![]() 次,得到如下统计表:
次,得到如下统计表:
①生产![]() 件甲产品和
件甲产品和![]() 件乙产品
件乙产品
正次品 | 甲正品 甲正品 乙正品 | 甲正品 甲正品 乙次品 | 甲正品 甲次品 乙正品 | 甲正品 甲次品 乙次品 | 甲次品 甲次品 乙正品 | 甲次品 甲次品 乙次品 |
频 数 |
|
|
|
|
|
|
②生产![]() 件甲产品和
件甲产品和![]() 件乙产品
件乙产品
正次品 | 乙正品 乙正品 甲正品 | 乙正品 乙正品 甲次品 | 乙正品 乙次品 甲正品 | 乙正品 乙次品 甲次品 | 乙次品 乙次品 甲正品 | 乙次品 乙次品 甲次品 |
频 数 |
|
|
|
|
|
|
已知生产电子产品甲![]() 件,若为正品可盈利
件,若为正品可盈利![]() 元,若为次品则亏损
元,若为次品则亏损![]() 元;生产电子产品乙
元;生产电子产品乙![]() 件,若为正品可盈利
件,若为正品可盈利![]() 元,若为次品则亏损
元,若为次品则亏损![]() 元.
元.
(I)按方案①生产![]() 件甲产品和
件甲产品和![]() 件乙产品,求这
件乙产品,求这![]() 件产品平均利润的估计值;
件产品平均利润的估计值;
(II)从方案①②中选其一,生产甲乙产品共![]() 件,欲使
件,欲使![]() 件产品所得总利润大于
件产品所得总利润大于![]() 元的机会多,应选用哪个?
元的机会多,应选用哪个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com