练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在直三棱柱中， , 是的中点， 是的中点。

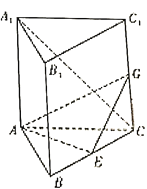
    （1）求异面直线与所成的角；

    （II）求证

    （III）求二面角的正切值.

    【答案】（1）（2）见解析（3）

    【解析】试题分析：（1）线线角找平移: 取的中点，则，所以是异面直线与所成的角,再根据余弦定理解得角（2）由三角形相似可得.再根据侧面与底面垂直, 得,即得；根据线面垂直判定定理得, (3) 设是的中点，过点作于，根据线面垂直判定定理以及性质定理可得为二面角平面角,再根据解三角形得二面角的正切值.

    试题解析：解：（I）取的中点，连，则，所以是异面直线与所成的角。设，则， ，

    .

    。在中，

    .所以异面直线与所成的角为.

    （II）由（I）可知， ,又因为三棱柱是直三棱柱，所以

    ,得；又由与相似，得又由

    ,所以, .

    （III）连接，设是的中点，过点作于，连,

    则.又由平面 平面,所以.

    由，得

    所以二面角的平面角正切值是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】解关于x的不等式ax2﹣（a+1）x+1＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】．已知函数

    （1）当时，求曲线在点处的切线方程；

    （2）求函数的极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y=x+sin|x|，x∈[﹣π，π]的大致图象是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在下列4个函数：① ；②y=sinx；③y=﹣tanx；④y=﹣cos2x、其中在区间 上增函数且以π为周期的函数是（把所有符合条件的函数序列号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： + =1（a＞b＞0），短轴长2，两焦点分别为F1 ， F2 ， 过F1的直线交椭圆C于M，N两点，且△F2MN的周长为8．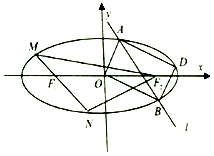

    （1）求椭圆C的方程；
    （2）直线l与椭圆C相交于A，B点，点D为椭圆C上一点，四边形AOBD为矩形，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在五面体中， , ,

    ， ，平面平面.

    （1） 证明: 直线平面；

    （2） 已知为棱上的点，试确定点位置，使二面角的大小为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了得到函数y=sin（2x﹣ ），x∈R的图象，只需将函数y=sin2x，x∈R的图象上所有的点（ ）
    A.向左平行移动 个单位长度
    B.向右平行移动 个单位长度
    C.向左平行移动 个单位长度
    D.向右平行移动 个单位长度

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱的所有棱长均为2，底面侧面， ， 为的中点， .

    （1）证明： .

    （2）若是棱上一点，满足，求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案