Question

【题目】如图某空间几何体的正视图和俯视图分别为边长为2的正方形和正三角形，则该空间几何体的外接球的表面积为（ ）
A.
B.
C.16π
D.21π

Answer 1

【答案】B
【解析】解：如图，由几何体的三视图知该几何体是四棱锥S﹣ABCD， 其中ABCD是边长为2的正方形，△SBC是边长为2 的等边三角形，
AB⊥平面SBC，
取BC中点F，AD中点E，连结SF，EF，取EF中点M，则MF=1，SF= ，
设该几何体外接球的球心为O，则OM⊥面ABCD，设OM=x，
过O作OH⊥SF，交SF于H，则SH= -x，OH=MF=1，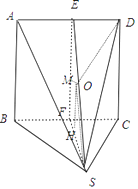

∴OD2=OS2=R2 ，
即（ ）2+x2=12+（ -x）2 ，
解得x= ，
∴R= = ，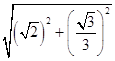
∴该空间几何体的外接球的表面积S= = ．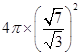
故选：B．
【考点精析】解答此题的关键在于理解简单空间图形的三视图的相关知识，掌握画三视图的原则：长对齐、高对齐、宽相等．