
如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=________时,CF⊥平面B1DF.

a或2a
【解析】法一:由已知得B1D⊥平面AC1,
又CF?平面AC1,∴B1D⊥CF,
故若CF⊥平面B1DF,则必有CF⊥DF.
设AF=x(0<x<3a),则CF2=x2+4a2,
DF2=a2+(3a-x)2,又CD2=a2+9a2=10a2,
∴10a2=x2+4a2+a2+(3a-x)2,
解得x=a或2a.
法二:分别以BA、BC、BB1所在直线为x轴、y轴、z轴建立空间直角坐标系B-xyz,
则B(0,0,0),B1(0,0,3a),设F( a,0,m),D
a,0,m),D ,C(0,
,C(0, a,0),
a,0),
 =(
=( a,-
a,- a,m),
a,m), =
= ,
,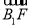 =(
=( a,0,m-3a),
a,0,m-3a),
∵CF⊥面B1DF,∴CF⊥B1F, ⊥
⊥ ,即
,即 ·
· =0,
=0,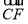 ·
·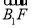 =0,
=0,
可得2a2+m(m-3a)=0,解得m=a或2a.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-10练习卷(解析版) 题型:填空题
为了调查某地居民的年收入x(单位:万元)和年饮食支出y(单位:万元)之间的关系,用分层抽样的方法从该地调查了若干户家庭,调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程为=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出增加________万元.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评7练习卷(解析版) 题型:选择题
使 n(n∈N*)的展开式中含有常数项的最小的n为( ).
n(n∈N*)的展开式中含有常数项的最小的n为( ).
A.4 B.5 C.6 D.7
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评6练习卷(解析版) 题型:选择题
已知0<θ< ,则双曲线C1:
,则双曲线C1: =1与C2:
=1与C2:
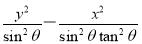 =1的( ).
=1的( ).
A.实轴长相等 B.虚轴长相等 C.焦距相等 D.离心率相等
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评5练习卷(解析版) 题型:解答题
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
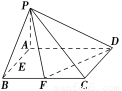
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评5练习卷(解析版) 题型:选择题
设m,n是空间两条直线,α,β是空间两个平面,则下列选项中不正确的是( ).
A.当n⊥α时,“n⊥β”是“α∥β”成立的充要条件
B.当m?α时,“m⊥β”是“α⊥β”的充分不必要条件
C.当m?α时,“n∥α”是“m∥n”必要不充分条件
D.当m?α时,“n⊥α”是“m⊥n”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(解析版) 题型:选择题
下面是关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;
p2:数列{nan}是递增数列;
p3:数列 是递增数列;
是递增数列;
p4:数列{an+3nd}是递增数列.其中的真命题为( ).
A.p1,p2 B.p3,p4 C.p2,p3 D.p1,p4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评1练习卷(解析版) 题型:解答题
若复数z1与z2在复平面上所对应的点关于y轴对称,且z1(3-i)=z2(1+3i),|z1|=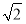 ,求z1.
,求z1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com