
ЁОЬтФПЁПЮЊМгПьаТФмдДЦћГЕВњвЕЗЂеЙ,ЭЦНјНкФмМѕХХ,ЙњМвЙФРјЯћЗбепЙКТђаТФмдДЦћГЕ.ФГаЃбаОПадбЇЯАаЁзщДгЦћГЕЪаГЁЩЯЫцЛњбЁШЁСЫMСОДПЕчЖЏГЫгУГЕ.ИљОнЦфајЪЛРяГЬR(ЕЅДЮГфЕчКѓФмааЪЛЕФзюДѓРяГЬ)зїГіСЫЦЕТЪгыЦЕЪ§ЕФЭГМЦБэ:
Зжзщ | ЦЕЪ§ | ЦЕТЪ |
80ЁмR<150 | 10 |
|
150ЁмR<250 | 30 | x |
RЁн250 | y | z |
КЯМЦ | M | 1 |
(1)Чѓx,y,z,MЕФжЕ;
(2)ШєгУЗжВуГщбљЕФЗНЗЈДгетMСОДПЕчЖЏГЫгУГЕжаГщШЁвЛИіШнСПЮЊ6ЕФбљБО,ДгИУбљБОжаШЮбЁ2СО,ЧѓбЁЕНЕФ2СОГЕајЪЛРяГЬЮЊ150ЁмR<250ЕФИХТЪ.
ЁОД№АИЁП(1) МћНтЮі.(2)![]() .
.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЦЕЪ§ЗжВМБэЃЌПЩЧѓЕУxЃЌyЃЌzЃЌMЕФжЕЃЛЃЈ2ЃЉСаОйГібљБОжаШЮбЁ2СОЙВга15жжШЁЗЈЃЌевЕНТњзуЬѕМўЕФЛљБОЪТМўЃЌдйРћгУЙХЕфИХаЭЕФИХТЪЕФЧѓЗЈНтЕУМДПЩЃЎ
ЪдЬтНтЮіЃК(1)гЩБэИёПЩжЊ![]() ,
,
ЫљвдM=60,x=![]() ,y=60-10-30=20,z=
,y=60-10-30=20,z=![]() .
.
(2)ЩшЁАДгет6СОДПЕчЖЏГЕжаШЮбЁ2СО,бЁЕНЕФ2СОГЕајЪЛРяГЬЮЊ150ЁмR<250ЁБЮЊЪТМўD,гЩЗжВуГщбљЕУдк80ЁмR<150жаГщ1СО,МЧЮЊA,дк150ЁмR<250жаГщ3СО,МЧЮЊB1,B2,B3,дкRЁн250жаГщ2СО,МЧЮЊC1,C2,дђШЮШЁСНСОЙВга15жжШЁЗЈ:(A,B1),(A,B2),(A,B3),(A,C1),(A,C2),(B1,B2),(B1,B3),(B2,B3),(B1,C1),(B1,C2),(B2,C1),(B2,C2),(B3,C1),(B3,C2),(C1,C2),ЪТМўDга3жжЧщПі,дђP(D)=![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЖЈвхгђЮЊ![]() ЕФКЏЪ§
ЕФКЏЪ§![]() ЃЌШчЙћЭЌЪБТњзувдЯТШ§ЬѕЃКЂйЖдШЮвтЕФ
ЃЌШчЙћЭЌЪБТњзувдЯТШ§ЬѕЃКЂйЖдШЮвтЕФ![]() ЃЌзмга
ЃЌзмга![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂлШє
ЃЛЂлШє![]() ЃЌЖМга
ЃЌЖМга![]() ГЩСЂЃЌдђГЦКЏЪ§
ГЩСЂЃЌдђГЦКЏЪ§![]() ЮЊРэЯыКЏЪ§ЃЎ
ЮЊРэЯыКЏЪ§ЃЎ
(1) ШєКЏЪ§![]() ЮЊРэЯыКЏЪ§ЃЌЧѓ
ЮЊРэЯыКЏЪ§ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(2)ХаЖЯКЏЪ§![]()
![]() ЪЧЗёЮЊРэЯыКЏЪ§ЃЌВЂгшвджЄУїЃЛ
ЪЧЗёЮЊРэЯыКЏЪ§ЃЌВЂгшвджЄУїЃЛ
(3) ШєКЏЪ§![]() ЮЊРэЯыКЏЪ§ЃЌ
ЮЊРэЯыКЏЪ§ЃЌ![]() МйЖЈ
МйЖЈ![]()
![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
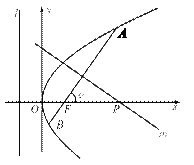
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЩЯвЛЕу
ЩЯвЛЕу![]() ЕННЙЕу
ЕННЙЕу![]() ЕФОрРы
ЕФОрРы![]() ЃЌЧуаБНЧ
ЃЌЧуаБНЧ
ЮЊ![]() ЕФжБЯпОЙ§НЙЕу
ЕФжБЯпОЙ§НЙЕу![]() ЃЌЧвгыХзЮяЯпНЛгк
ЃЌЧвгыХзЮяЯпНЛгк![]() ЁЂ
ЁЂ![]() СНЕу.
СНЕу.
ЃЈ1ЃЉЧѓХзЮяЯпЕФБъзМЗНГЬМАзМЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШє![]() ЮЊШёНЧЃЌзїЯпЖЮ
ЮЊШёНЧЃЌзїЯпЖЮ![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌжЄУї
ЃЌжЄУї![]() ЮЊЖЈжЕЃЌВЂЧѓДЫЖЈжЕ.
ЮЊЖЈжЕЃЌВЂЧѓДЫЖЈжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГТУгЮАЎКУепМЦЛЎДг3ИібЧжоЙњМвA1ЃЌA2ЃЌA3КЭ3ИіХЗжоЙњМвB1ЃЌB2ЃЌB3жабЁдё2ИіЙњМвШЅТУгЮ.
(1)ШєДгет6ИіЙњМвжаШЮбЁ2ИіЃЌЧѓет2ИіЙњМвЖМЪЧбЧжоЙњМвЕФИХТЪЃЛ
(2)ШєДгбЧжоЙњМвКЭХЗжоЙњМвжаИїбЁ1ИіЃЌЧѓетСНИіЙњМвАќРЈA1ЃЌЕЋВЛАќРЈB1ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЭХЮЏзщжЏСЫЁАЮФУїГіааЃЌАЎЮвжаЛЊЁБЕФжЊЪЖОКШќЃЌДгВЮМгПМЪдЕФбЇЩњжаГщГі60УћбЇЩњЃЌНЋЦфГЩМЈЃЈЕЅЮЛЃКЗжЃЉећРэКѓЃЌЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМЃЈЦфжаЗжзщЧјМфЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЉ.
ЃЉ.

ЃЈ1ЃЉЧѓГЩМЈдк![]() ЕФЦЕТЪЃЌВЂВЙШЋДЫЦЕТЪЗжВМжБЗНЭМЃЛ
ЕФЦЕТЪЃЌВЂВЙШЋДЫЦЕТЪЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉЧѓетДЮПМЪдЦНОљЗжЕФЙРМЦжЕЃЛ
ЃЈ3ЃЉШєДгГЩМЈдк![]() КЭ
КЭ![]() ЕФбЇЩњжаШЮбЁСНШЫЃЌЧѓЫћУЧЕФГЩМЈдкЭЌвЛЗжзщЧјМфЕФИХТЪ.
ЕФбЇЩњжаШЮбЁСНШЫЃЌЧѓЫћУЧЕФГЩМЈдкЭЌвЛЗжзщЧјМфЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЧѓ
ЃЉЧѓ![]() ЕФжЕгђ
ЕФжЕгђ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉШєЖдгк
ЃЉШєЖдгк![]() ФкЕФЫљгаЪЕЪ§
ФкЕФЫљгаЪЕЪ§![]() ЃЌВЛЕШЪН
ЃЌВЛЕШЪН![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§ ![]() ЃЌgЃЈxЃЉ=fЃЈxЃЉ+mЃЌШєКЏЪ§gЃЈxЃЉЧЁгаШ§ИіВЛЭЌСуЕуЃЌдђЪЕЪ§mЕФШЁжЕЗЖЮЇЮЊЃЈ ЃЉ
ЃЌgЃЈxЃЉ=fЃЈxЃЉ+mЃЌШєКЏЪ§gЃЈxЃЉЧЁгаШ§ИіВЛЭЌСуЕуЃЌдђЪЕЪ§mЕФШЁжЕЗЖЮЇЮЊЃЈ ЃЉ
A.ЃЈ1ЃЌ10ЃЉ
B.ЃЈЉ10ЃЌЉ1ЃЉ
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшfЃЈxЃЉ=sinxcosxЉcos2ЃЈx+ ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓfЃЈxЃЉЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉдкШёНЧЁїABCжаЃЌНЧAЃЌBЃЌCЕФЖдБпЗжБ№ЮЊaЃЌbЃЌcЃЌШєfЃЈ ![]() ЃЉ=0ЃЌa=1ЃЌЧѓЁїABCУцЛ§ЕФзюДѓжЕЃЎ
ЃЉ=0ЃЌa=1ЃЌЧѓЁїABCУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com