
【题目】已知e为自然对数的底数,设函数![]() ,则( ).
,则( ).
A. 当k=1时,f(x)在x=1处取到极小值 B. 当k=1时,f(x)在x=1处取到极大值
C. 当k=2时,f(x)在x=1处取到极小值 D. 当k=2时,f(x)在x=1处取到极大值
【答案】C
【解析】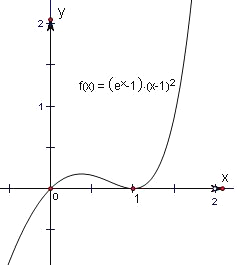
当k=1时,函数f(x)=(ex1)(x1).
求导函数可得f′(x)=ex(x1)+(ex1)=(xex1)
f′(1)=e1≠0,f′(2)=2e21≠0,
则f(x)在在x=1处与在x=2处均取不到极值,
当k=2时,函数f(x)=(ex1)(x1)2.
求导函数可得f′(x)=ex(x1)2+2(ex1)(x1)=(x1)(xex+ex2)
∴当x=1,f′(x)=0,且当x>1时,f′(x)>0,当x0<x<1时(x0为极大值点),f′(x)<0,故函数f(x)在(1,+∞)上是增函数;在(x0,1)上是减函数,从而函数f(x)在x=1取得极小值。对照选项。
故选C.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 如果平面![]() 外的直线
外的直线![]() 不平行于平面
不平行于平面![]() ,则平面
,则平面![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
B. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么直线
,那么直线![]() 平面
平面![]()
C. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
D. 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且
,且![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的顶点
的顶点![]() 作两条互相垂直的直线与椭圆分别相交于
作两条互相垂直的直线与椭圆分别相交于![]() 两点.若
两点.若![]() 的角平分线方程为
的角平分线方程为![]() ,求
,求![]() 的面积及直线
的面积及直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上半年产品产量与单位成本资料如下:
月份 | 产量/千件 | 单位成本/元 |
1 | 2 | 73 |
2 | 3 | 72 |
3 | 4 | 71 |
4 | 3 | 73 |
5 | 4 | 69 |
6 | 5 | 68 |
且已知产量x与单位成本y具有线性相关关系.
(1)求出回归方程.
(2)指出产量每增加1 000件时,单位成本平均变动多少?
(3)假定产量为6 000件时,单位成本为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() ,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在调查运动员是否服用过兴奋剂的时候,给出两个问题作答,无关紧要的问题是:“你的身份证号码的尾数是奇数吗?”敏感的问题是:“你服用过兴奋剂吗?”然后要求被调查的运动员掷一枚硬币,如果出现正面,就回答第一个问题,否则回答第二个问题.由于回答哪一个问题只有被测试者自己知道,所以应答者一般乐意如实地回答问题.若我们把这种方法用于300个被调查的运动员,得到80个“是”的回答,则这群运动员中服用过兴奋剂的百分率大约为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com