
【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 |
P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元,X表示经销一件该商品的利润.
(1)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率![]() ;
;
(2)求X的分布列及期望![]() .
.
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
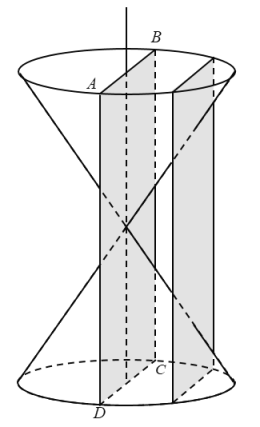
【题目】古希腊数学家阿波罗尼奥斯在他的著作《圆锥曲线论》中记载了用平面切制圆锥得到圆锥曲线的方法.如图,将两个完全相同的圆锥对顶放置(两圆锥的轴重合),已知两个圆锥的底面半径为1,母线长均为![]() ,记过圆锥轴的平面ABCD为平面
,记过圆锥轴的平面ABCD为平面![]() (
(![]() 与两个圆锥面的交线为AC、BD),用平行于
与两个圆锥面的交线为AC、BD),用平行于![]() 的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高速公路全程设有2n(n≥4,![]() )个服务区.为加强驾驶人员的安全意识,现规划在每个服务区的入口处设置醒目的宣传标语A或宣传标语B.
)个服务区.为加强驾驶人员的安全意识,现规划在每个服务区的入口处设置醒目的宣传标语A或宣传标语B.
(1)若每个服务区入口处设置宣传标语A的概率为![]() ,入口处设置宣传标语B的服务区有X个,求X的数学期望;
,入口处设置宣传标语B的服务区有X个,求X的数学期望;
(2)试探究全程两种宣传标语的设置比例,使得长途司机在走该高速全程中,随机选取3个服务区休息,看到相同宣传标语的概率最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,
,![]() 分别是曲线
分别是曲线![]() ,
,![]() 上两动点且
上两动点且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,
,![]() 分别是曲线
分别是曲线![]() ,
,![]() 上两动点且
上两动点且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用 y(万元),有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料可知y对x呈线性相关关系,且线性回归方程为y=a+bx,其中已知b=1.23,请估计使用年限为20年时,维修费用约为_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com