
分析 若函数f(x)在[m,n](m<n)上的值域恰好为[m,n],则称f(x)为函数的一个“等值映射区间”.根据新定义可知,“等值映射区间”即是函数与另一函数y=x有两个交点.即可判断.
解答 解:根据新定义可知,“等值映射区间”即是函数与另一函数y=x有两个交点.[m,n](m<n)上的值域恰好为[m,n],可见[m,n]是单调递增.
对于(1)y=x2-1;根据新定义可得:x2-1=x,方程有两个解,即函数y=x2-1与函数y=x有两个交点.但在同一增区间上只有一个,故①不是;
对于(2)y=2+log2x;根据新定义可得:2+log2x=x,即函数y=2+log2x与函数y=x有两个交点.且在定义域内都是递增,故②是;
对于(3)y=2x-1;根据新定义可得:2x-1=x,即函数y=2x-1与函数y=x有两个交点.且在定义域内都是递增,故③是;
对于(4)y=$\frac{1}{x-1}$;根据新定义可得:x2-x=1,方程有两个解,即函数y=$\frac{1}{x-1}$与函数y=x有两个交点.但在同一增区间是只有一个,故④不是;
故答案为:(2),(3)
点评 本题考查了新定义的理解和定义域,值域的关系的运用.属于中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
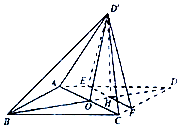 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.
如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
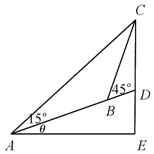 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.求此山对于地平面的倾斜角θ的余弦值.
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测得斜度为45°,建筑物的高CD为50米.求此山对于地平面的倾斜角θ的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点$({\frac{π}{3},0})$对称 | B. | 关于点$({\frac{2π}{3},0})$对称 | ||
| C. | 关于直线$x=\frac{π}{3}$对称 | D. | 关于直线$x=\frac{π}{6}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个正面和最多一个正面 | B. | 最多两个正面和至少两个正面 | ||
| C. | 不多于一个正面和至少两个正面 | D. | 至少两个正面和恰有一个正面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com