
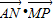 的取值范围为 .
的取值范围为 .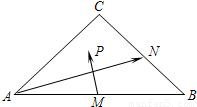
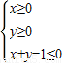
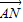 =(-1,
=(-1, ),
),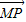 =(x-
=(x- ,y-
,y- )
)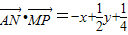 ,
,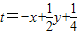 ,结合线性规划知识,
,结合线性规划知识,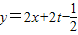
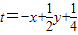 经过点A(1,0)时,
经过点A(1,0)时,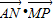 有最小值,
有最小值, ,
,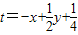 经过点B时,
经过点B时,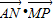 有最小值,
有最小值, ,
, ,
, ].
].

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
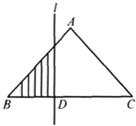 如图,在等腰直角三角形ABC中,BC=4,当一条垂直于底边BC(垂足为D)的直线l从左至右移动(与直角三角形ABC有公共点)时,直线l把直角三角形分成两部分,令BD=x,试写出图中阴影部分的面积y与x的函数关系式.
如图,在等腰直角三角形ABC中,BC=4,当一条垂直于底边BC(垂足为D)的直线l从左至右移动(与直角三角形ABC有公共点)时,直线l把直角三角形分成两部分,令BD=x,试写出图中阴影部分的面积y与x的函数关系式.查看答案和解析>>
科目:高中数学 来源:2012-2013学年内蒙古包头33中高二(上)期中数学试卷(文科)(解析版) 题型:选择题
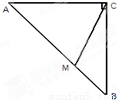
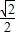



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com