
【题目】已知数列{an}满足,an+1=an+1![]() ,a1=a,则一定存在a,使数列中( )
,a1=a,则一定存在a,使数列中( )
A.存在n∈N*,有an+1an+2<0
B.存在n∈N*,有(an+1﹣1)(an+2﹣1)<0
C.存在n∈N*,有![]()
D.存在n∈N*,有![]()
科目:高中数学 来源: 题型:
【题目】2019年郑开国际马拉松比赛,于2019年3月31日在郑州、开封举行.某学校本着“我运动,我快乐,我锻炼,我提高”精神,积极组织学生参加比赛及相关活动,为了了解学生的参与情况,从全校学生中随机抽取了150名学生,对是否参与的情况进行了问卷调查,统计数据如下:
会参与 | 不会参与 | |
男生 | 60 | 40 |
女生 | 20 | 30 |
(1)根据上表说明,能否有97.5%的把握认为参与马拉松赛事与性别有关?
(2)现从参与问卷调查且参与赛事的学生中,采用按性别分层抽样的方法选取8人参加2019年马拉松比赛志愿者宣传活动,
①求男、女学生各选取多少人;
②若从这8人中随机选取2人到校广播站开展2019年赛事宣传介绍,求恰好选到2名男生的概率.
附:参考公式:![]() ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的四个顶点,过E的左焦点F且不与坐标轴垂直的直线l与E交于A,B两点,线段AB的垂直平分线m与x轴,y轴分别交于M,N两点,交线段AB于点C.
的短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的四个顶点,过E的左焦点F且不与坐标轴垂直的直线l与E交于A,B两点,线段AB的垂直平分线m与x轴,y轴分别交于M,N两点,交线段AB于点C.
(1)求E的方程;
(2)设O为坐标原点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,且
,且![]() ,当
,当![]() 时,求l的斜率的取值范围.
时,求l的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C的渐近线方程为![]() ,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣tx+t.
(1)讨论f(x)的单调性;
(2)当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若以
两点,若以![]() ,
,![]() 为邻边的平行四边形
为邻边的平行四边形![]() 的顶点
的顶点![]() 在椭圆
在椭圆![]() 上,求证:平行四边形
上,求证:平行四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是九江市2019年4月至2020年3月每月最低气温与最高气温(℃)的折线统计图:已知每月最低气温与最高气温的线性相关系数r=0.83,则下列结论错误的是( )
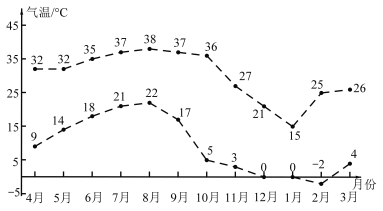
A.每月最低气温与最高气温有较强的线性相关性,且二者为线性正相关
B.月温差(月最高气温﹣月最低气温)的最大值出现在10月
C.9﹣12月的月温差相对于5﹣8月,波动性更大
D.每月最高气温与最低气温的平均值在前6个月逐月增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com