
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥
的正方形,△ABE和△BCF均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.
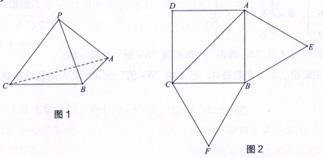
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】试题分析:第一问取![]() 中点
中点![]() ,根据等腰三角形的性质求得
,根据等腰三角形的性质求得![]() ,根据题中所给的边长,利用勾股定理求得
,根据题中所给的边长,利用勾股定理求得![]() ,利用线面垂直的判定定理以及面面垂直的判定定理得到结果;第二问根据题中所给的条件建立空间直角坐标系,写出相应的点的坐标,求得面的法向量,利用法向量所成角的余弦值得出结果;第三问利用向量间的关系,利用向量垂直的条件,利用向量的数量积等于0,得出所求的比值
,利用线面垂直的判定定理以及面面垂直的判定定理得到结果;第二问根据题中所给的条件建立空间直角坐标系,写出相应的点的坐标,求得面的法向量,利用法向量所成角的余弦值得出结果;第三问利用向量间的关系,利用向量垂直的条件,利用向量的数量积等于0,得出所求的比值![]() 与
与![]() 的关系式,利用函数的有关知识求得结果.
的关系式,利用函数的有关知识求得结果.
(Ⅰ)方法1:
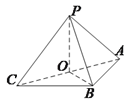
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() . 由题意
. 由题意
![]() ,
, ![]() ,
, ![]()
因为在![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点
的中点
所以![]() ,
,
因为在![]() 中,
中, ![]() ,
, ![]() ,
, ![]()
所以![]()
因为![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以平面![]()
![]() 平面
平面![]()
方法2:

设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() .
.
因为在![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点
的中点
所以![]() ,
,
因为![]() ,
, ![]() ,
, ![]()
所以![]() ≌
≌![]() ≌
≌![]()
所以![]()
所以![]()
因为![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以平面![]()
![]() 平面
平面![]()
方法3:
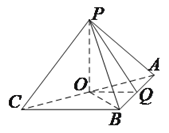
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,因为在
,因为在![]() 中,
中, ![]() ,
,
所以![]()
设![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() 及
及![]() .
.
因为在![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点
的中点
所以![]() .
.
因为在![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点
的中点
所以![]() .
.
因为![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以![]()
因为![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]()
所以平面![]()
![]() 平面
平面![]()
(Ⅱ)由![]() 平面
平面![]() ,
, ![]() ,如图建立空间直角坐标系,则
,如图建立空间直角坐标系,则
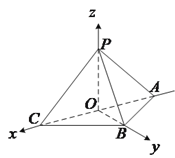
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
由![]() 平面
平面![]() ,故平面
,故平面![]() 的法向量为
的法向量为![]()
由![]() ,
, ![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由![]() 得:
得: ![]()
令![]() ,得
,得![]() ,
, ![]() ,即
,即![]()
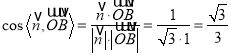
由二面角![]() 是锐二面角,
是锐二面角,
所以二面角![]() 的余弦值为
的余弦值为![]()
(Ⅲ)设![]() ,
, ![]() ,则
,则
![]()
![]()
令![]()
得![]()
即![]() ,μ是关于λ的单调递增函数,
,μ是关于λ的单调递增函数,
当![]() 时,
时, ![]() ,
,
所以![]()


科目:高中数学 来源: 题型:
【题目】小王想进行理财投资,根据长期收益率市场顶测,投资A类产品和B类产品的收益分别为![]() (万元),它们与投资额x(万元)存在如下关系式:
(万元),它们与投资额x(万元)存在如下关系式:![]() ,
,![]() ,小王准备将200万元资金投入A、B两类理财产品,公司要求每类产品的投资金额不能低于25万元
,小王准备将200万元资金投入A、B两类理财产品,公司要求每类产品的投资金额不能低于25万元
(1)若对B类产品的投资金额为x(万元),求总收益y(万元)关于x的函数关系式;
(2)请你帮助小王预算如何分配投资资金,才能使总收益最大,并求出最大总收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年中央电视台春节联欢晚会分会场之一落户黔东南州黎平县肇兴侗寨,黔东南州某中学高二社会实践小组就社区群众春晚节目的关注度进行了调查,随机抽取80名群众进行调查,将他们的年龄分成6段: ![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
(Ⅰ)求这80名群众年龄的中位数;
(Ⅱ)将频率视为概率,现用随机抽样方法从该社区群众中每次抽取1人,共抽取3次,记被抽取的3人中年龄在![]() 的人数为
的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,及数学期望
的分布列,及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某名校从![]() 年到
年到![]() 年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将
年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将![]() 年编号为
年编号为![]() ,
,![]() 年编为
年编为![]() ,以此类推……)
,以此类推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)将这![]() 年的数据分为人数不少于
年的数据分为人数不少于![]() 人和少于
人和少于![]() 人两组,按分层抽样抽取
人两组,按分层抽样抽取![]() 年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这
年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这![]() 年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于
年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于![]() 的概率是多少?;
的概率是多少?;
(2)根据最近![]() 年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测
年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测![]() 年该校考入清华、北大的人数。(结果要求四舍五入至个位)
年该校考入清华、北大的人数。(结果要求四舍五入至个位)
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为![]() 内一点,若分别满足①
内一点,若分别满足①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (其中
(其中![]() 为
为![]() 中,角
中,角![]() 所对的边).则O依次是
所对的边).则O依次是![]() 的( )
的( )
A.内心、重心、垂心、外心B.外心、垂心、重心、内心
C.外心、内心、重心、垂心D.内心、垂心、外心、重心
查看答案和解析>>
科目:高中数学 来源: 题型:
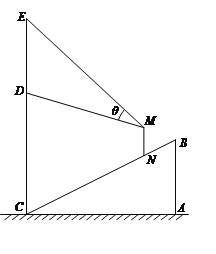
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米,最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ.
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米时,视角θ最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点.(1)若
的焦点.(1)若![]() 为椭圆
为椭圆![]() 上两点,且线段
上两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于![]() 和
和![]() ,设线段
,设线段![]() 的长分别为
的长分别为![]() ,证明
,证明![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在标有“甲”的袋中有![]() 个红球和
个红球和![]() 个白球,这些球除颜色外完全相同.
个白球,这些球除颜色外完全相同.
(Ⅰ)若从袋中依次取出![]() 个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
(Ⅱ)现从甲袋中取出个![]() 红球,
红球, ![]() 个白球,装入标有“乙”的空袋.若从甲袋中任取
个白球,装入标有“乙”的空袋.若从甲袋中任取![]() 球,乙袋中任取
球,乙袋中任取![]() 球,记取出的红球的个数为
球,记取出的红球的个数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电力公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行综合排序,综合排序高者中标。分值权重表如下:
总分 | 技术 | 商务 | 报价 |
100% | 50% | 10% | 40% |
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的。报价表则相对灵活,报价标的评分方法是:基准价的基准分是68分,若报价每高于基准价1%,则在基准分的基础上扣0.8分,最低得分48分;若报价每低于基准价1%,则在基准分的基础上加0.8分,最高得分为80分。若报价低于基准价15%以上(不含15%)每再低1%,在80分在基础上扣0.8分。在某次招标中,若基准价为1000(万元)。甲、乙两公司综合得分如下表:
公司 | 技术 | 商务 | 报价 |
甲 | 80分 | 90分 |
|
乙 | 70分 | 100分 |
|
甲公司报价为1100(万元),乙公司的报价为800(万元)则甲,乙公司的综合得分,分别是
A. 73,75.4 B. 73,80 C. 74.6,76 D. 74.6 ,75.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com