练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=﹣f'（0）ex+2x，点P为曲线y=f（x）在点（0，f（0））处的切线l上的一点，点Q在曲线y=ex上，则|PQ|的最小值为 ．

    【答案】
    【解析】解：f（x）=﹣f'（0）ex+2x， 可得f′（x）=﹣f'（0）ex+2，
    即有f′（0）=﹣f'（0）e0+2，
    解得f′（0）=1，
    则f（x）=﹣ex+2x，
    f（0）=﹣e0+0=﹣1，
    则切线l：y=x﹣1，
    y=ex的导数为y′=ex ，
    过Q的切线与切线l平行时，距离最短．
    由ex=1，可得x=0，
    即切点Q（0，1），
    则Q到切线l的距离为 = ．
    故答案为： ．
    求出f（x）的导数，令x=0，可得切线l的斜率和切点，切线方程l，再求y=ex导数，由过Q的切线与切线l平行时，距离最短．求得切点Q的坐标，运用点到直线的距离公式，即可得到最小值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知 ，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，AB=1，BC=2，∠CBA= ，ABEF为直角梯形，BE∥AF，∠BAF= ，BE=2，AF=3，平面ABCD⊥平面ABEF．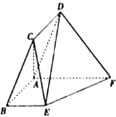

    （1）求证：AC⊥平面ABEF；
    （2）求平面ABCD与平面DEF所成二面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=ax﹣x3（a＞0，且a≠1）恰好有两个不同的零点，则实数a的取值范围是（ ）
    A.1＜a＜e
    B.1＜a＜e
    C.0＜a＜e
    D.e ＜a＜e

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在5件产品中，有3件一等品和2件二等品，从中任取2件，那么以 为概率的事件是（ ）
    A.都不是一等品
    B.恰有一件一等品
    C.至少有一件一等品
    D.至多一件一等品

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 ，数列{an}的前n项的和记为Sn ．
    （1）求S1 ， S2 ， S3的值，猜想Sn的表达式；
    （2）请用数学归纳法证明你的猜想．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a，b，c分别是内角A，B，C的对边，且（a+c）2=b2+3ac
    （Ⅰ）求角B的大小；
    （Ⅱ）若b=2，且sinB+sin（C﹣A）=2sin2A，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线2x+y﹣k=0（k＞0）与圆x2+y2=4交于不同的两点A，B，O是坐标原点，且有| | | |，那么k的取值范围是（ ）
    A.[ ，+∞）
    B.[ ，2 ）
    C.[ ，+∞）
    D.[ ，2 ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个不透明的袋子装有4个完全相同的小球，球上分别标有数字为0，1，2，2，现甲从中摸出一个球后便放回，乙再从中摸出一个球，若摸出的球上数字大即获胜（若数字相同则为平局），则在甲获胜的条件下，乙摸1号球的概率为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案