
【题目】已知函数f(x)=log ![]() .
.
(1)求f(x)的定义域;
(2)求f(x)的值域.
【答案】
(1)解:函数f(x)=log ![]() .
.
定义域需满足: ![]() ,即﹣x2+2x+8>0
,即﹣x2+2x+8>0
解得:﹣2<x<4
∴f(x)的定义域为{x|﹣2<x<4}
(2)解:设u=﹣x2+2x+8,对数的底数小于1,根据性质可知,函数f(x)= ![]() 是减函数,
是减函数,
函数u=﹣x2+2x+8=﹣(x+1)2+9,t= ![]()
∴0<u≤9
∴0<t≤3,
∵f(x)= ![]() 在(0,+∞)减函数,
在(0,+∞)减函数,
∴f(x)的值域是[ ![]() ,+∞)
,+∞)
【解析】(1)由真数大于零即不等式即可得到函数的定义域。(2)利用复合函数的性质结合二次函数的最值情况即可得出函数的值域。
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识,掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零,以及对函数的值域的理解,了解求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零,以及对函数的值域的理解,了解求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.


科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2 ![]() ,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 .
,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 . 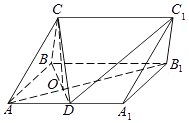
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线CD与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
(a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,只需将函数y=sin2x的图象上所有的点( )
)的图象,只需将函数y=sin2x的图象上所有的点( )
A.向左平移 ![]() 个单位
个单位
B.向左平移 ![]() 个单位
个单位
C.向右平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
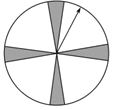
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.
乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.问:购买该商品的顾客在哪家商场中奖的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在直线y=4x上,且与直线l:x+y﹣2=0相切于点P(1,1)
(Ⅰ)求圆的方程
(II)直线kx﹣y+3=0与该圆相交于A、B两点,若点M在圆上,且有向量 ![]() (O为坐标原点),求实数k.
(O为坐标原点),求实数k.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com