
【题目】已知定义域为![]() 的函数
的函数![]() 的图象为曲线
的图象为曲线![]() ,曲线
,曲线![]() 在点
在点![]() 的切线为
的切线为![]() (其中
(其中![]() ).
).
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)证明:(i)![]() ;
;
(ii)![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)(
;(Ⅱ)(![]() )证明见解析,(ii)证明见解析
)证明见解析,(ii)证明见解析
【解析】
(Ⅰ)根据导数的几何意义可写出曲线![]() 在
在![]() 处的切线方程,进而求得实数
处的切线方程,进而求得实数![]() 的值;
的值;
(Ⅱ)(i)令![]() ,对
,对![]() 求导,利用导数求函数
求导,利用导数求函数![]() 的单调性,即可得证;
的单调性,即可得证;
(ii)当![]() 时,证明
时,证明![]() ,构造
,构造![]() ,求导得到单调区间,计算最值得证,即
,求导得到单调区间,计算最值得证,即![]() ,联合(i)中结论得到答案.
,联合(i)中结论得到答案.
(Ⅰ)![]() ,于是
,于是![]() ,
,
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
整理得![]() ,所以可得
,所以可得![]() .
.
(Ⅱ)证明:(![]() )令
)令![]() ,则
,则![]() ,
,
易知当![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减,
单调递减,
所以![]() ,所以
,所以![]() .
.
(ii)由(Ⅰ)可知![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() .
.
因为![]() 过点
过点![]() ,且
,且![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
故可猜测:
当![]() 时,
时,![]() 的图象恒在切线
的图象恒在切线![]() 的上方.
的上方.
下证:当![]() 时,
时,![]() .
.
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,/p>
,/p>
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
又![]() ,所以
,所以![]() ,
,
所以存在![]() ,使得
,使得![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
又![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
故![]() .
.
又由(i)可得![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时,等号成立.
时,等号成立.


科目:高中数学 来源: 题型:
【题目】设V是空间中2019个点构成的集合,其中任意四点不共面某些点之间连有线段,记E为这些线段构成的集合.试求最小的正整数n,满足条件:若E至少有n个元素,则E一定含有908个二元子集,其中每个二元子集中的两条线段有公共端点,且任意两个二元子集的交为空集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三位数中,如果百位数字、十位数字、个位数字刚好能构成等差数列,则称为“等差三位数”,例如:147,642,777,420等等.等差三位数的总个数为( )
A.32B.36C.40D.45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一个最高点为(![]() ),与之相邻的一个对称中心为
),与之相邻的一个对称中心为![]() ,将f(x)的图象向右平移
,将f(x)的图象向右平移![]() 个单位长度得到函数g(x)的图象,则( )
个单位长度得到函数g(x)的图象,则( )
A.g(x)为偶函数
B.g(x)的一个单调递增区间为![]()
C.g(x)为奇函数
D.函数g(x)在![]() 上有两个零点
上有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:![]() 和圆C2:(x-6)2+(y-1)2=1,过圆C2上一点P作圆的切线MN交抛物线C,于M,N两点,若点P为MN的中点,则切线MN的斜率k>1时的直线方程为( )
和圆C2:(x-6)2+(y-1)2=1,过圆C2上一点P作圆的切线MN交抛物线C,于M,N两点,若点P为MN的中点,则切线MN的斜率k>1时的直线方程为( )
A.4x-3y-22=0B.4x-3y-16=0C.2x-y-11+5=0D.4x-3y-26=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为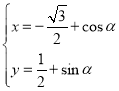 (
(![]() 为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)设射线l的极坐标方程为![]() ,若射线l与曲线C交于A,B两点,求AB的长;
,若射线l与曲线C交于A,B两点,求AB的长;
(2)设M,N是曲线C上的两点,若∠MON![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

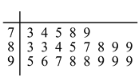
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com