
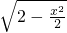 在(0,2)内具有“Lg”性质,且中值ξ=
在(0,2)内具有“Lg”性质,且中值ξ= ,f′(ξ)=-
,f′(ξ)=- ;
; [f(x1)+f(x2)]<f(
[f(x1)+f(x2)]<f( )恒成立,则函数f(x)在(a,b)内具有“Lg”性质,且必有中值ξ=
)恒成立,则函数f(x)在(a,b)内具有“Lg”性质,且必有中值ξ= .
. 时的导数值与之相等,对于③,举反例进行判定即可,对于④,只能保证f(x)是上凸函数,不能保证中值一定在中点处进行判定.
时的导数值与之相等,对于③,举反例进行判定即可,对于④,只能保证f(x)是上凸函数,不能保证中值一定在中点处进行判定.
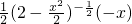 ,当x=
,当x= 时,y'=-
时,y'=- ,故②正确.
,故②正确. [f(x1)+f(x2)]<f(
[f(x1)+f(x2)]<f( )只能保证f(x)是上凸函数,不能保证中值一定在中点处.④错误
)只能保证f(x)是上凸函数,不能保证中值一定在中点处.④错误

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
2-
|
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
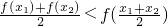 恒成立;
恒成立; 恒成立.
恒成立.查看答案和解析>>
科目:高中数学 来源:2010年四川省成都市高考数学三模试卷(理科)(解析版) 题型:解答题
 在(0,2)内具有“Lg”性质,且中值ξ=
在(0,2)内具有“Lg”性质,且中值ξ= ,f′(ξ)=-
,f′(ξ)=- ;
; [f(x1)+f(x2)]<f(
[f(x1)+f(x2)]<f( )恒成立,则函数f(x)在(a,b)内具有“Lg”性质,且必有中值ξ=
)恒成立,则函数f(x)在(a,b)内具有“Lg”性质,且必有中值ξ= .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com