
| 组别 | A | B | C |
| 人数 | 100 | 150 | 50 |
分析 (I)先求出样本容量与总体容量的比,由此能求出A,B,C三个组各选出的代表的个数.
(II)设来自A,B,C三个组的代表分别为a1,a2,b1,b2,b3,c.利用列举法能求出这两名代表来自同一组的概率.
(III)利用等可能事件概率计算公式能得到P2>P1.
解答 (本小题满分14分)
解:(I)因为样本容量与总体容量的比是$\frac{6}{100+150+50}=\frac{1}{50}$,
所以A,B,C三个组各选出的代表的数量分别为:$100×\frac{1}{50}=2,150×\frac{1}{50}=3,50×\frac{1}{50}=1$.
所以A,B,C三个组各选出的代表的个数分别为2,3,1.…(4分)
(II)设来自A,B,C三个组的代表分别为a1,a2,b1,b2,b3,c.
则从6名代表中任意取出两人的所有结果所构成的基本事件空间:
Ω={(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,c),(a2,b1),
(a2,b2),(a2,b3),(a2,c),(b1,b2),(b1,b3),(b1,c),
(b2,b3),(b2,c),(b3,c)},共15个基本事件.
记事件D=“抽出的两个代表来自同一组”.
则D={(a1,a2),(b1,b2),(b1,b3),(b2,b3)},共4个基本事件.
所以这两名代表来自同一组的概率${P_1}=\frac{4}{15}$.…(11分)
(III)P2>P1.…(14分)
点评 本题考查概率的求法,考查分层抽样的应用,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={(\frac{1}{2})^x}$ | B. | y=-x2 | C. | y=log2x | D. | y=|x|+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
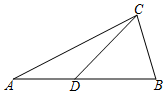 如图所示,点D 在线段AB 上,∠CAD=30°,∠CDB=50°.给出下列三组条件(给出线段的长度):
如图所示,点D 在线段AB 上,∠CAD=30°,∠CDB=50°.给出下列三组条件(给出线段的长度):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com