
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥![]() ,其中
,其中![]() .
.
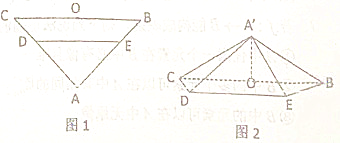
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某公园内有一块以![]() 为圆心半径为
为圆心半径为![]() 米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形
米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形![]() 区域,其中两个端点
区域,其中两个端点![]() ,
,![]() 分别在圆周上;观众席为梯形
分别在圆周上;观众席为梯形![]() 内切在圆
内切在圆![]() 外的区域,其中
外的区域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在点
在点![]() 的同侧.为保证视听效果,要求观众席内每一个观众到舞台
的同侧.为保证视听效果,要求观众席内每一个观众到舞台![]() 处的距离都不超过
处的距离都不超过![]() 米.设
米.设![]() ,
,![]() .问:对于任意
.问:对于任意![]() ,上述设计方案是否均能符合要求?
,上述设计方案是否均能符合要求?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习小组由学生和教师组成,人员构成同时满足以下三个条件:①男生人数多于女生人数;②女生人数多于教师人数;③教师人数的两倍多于男生人数.问:
(1)若教师人数为4,则女生人数的最大值为多少?
(2)该小组人数的最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() .
.
(1)若直线![]() 过点
过点![]() 且到圆心
且到圆心![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 的斜率为负),当
的斜率为负),当![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com