
| A. | (-∞,$\frac{1}{e}$] | B. | (-∞,e] | C. | $({\frac{1}{e},+∞})$ | D. | (e,+∞) |
分析 若?x∈(0,+∞),不等式ax-lnx>0恒成立,则a>$\frac{lnx}{x}$恒成立,令f(x)=$\frac{lnx}{x}$,利用导数法研究其最值,可得答案.
解答 解:若?x∈(0,+∞),不等式ax-lnx>0恒成立,
则a>$\frac{lnx}{x}$恒成立,
令f(x)=$\frac{lnx}{x}$,则f′(x)=$\frac{1-lnx}{{x}^{2}}$,
当x∈(0,e)时,f′(x)>0,f(x)为增函数;
当x∈(e,+∞)时,f′(x)<0,f(x)为减函数;
故当x=e时,f(x)=$\frac{lnx}{x}$取最大值$\frac{1}{e}$.
故a∈$({\frac{1}{e},+∞})$.
故选:C
点评 本题以命题的真假判断与应用为载体,考查了四种命题,复合命题,充要条件,特称命题,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.544 | B. | 0.68 | C. | 0.8 | D. | 0.85 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
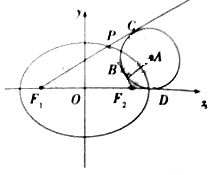 如图,F1,F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦点,椭圆的离心率为$\sqrt{3}$-1,P为椭圆上第一象限内的一点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圆A与△PF1F2三边所在直线都相切,切点分别为B,C,D,则圆A的半径为( )
如图,F1,F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦点,椭圆的离心率为$\sqrt{3}$-1,P为椭圆上第一象限内的一点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圆A与△PF1F2三边所在直线都相切,切点分别为B,C,D,则圆A的半径为( )| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{3}$-6 | C. | 4$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
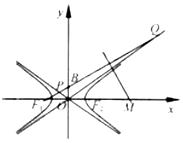 如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则双曲线C的渐近线方程是( )
如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则双曲线C的渐近线方程是( )| A. | y=±x | B. | $y=±\sqrt{3}x$ | C. | $y=±\frac{1}{2}x$ | D. | $y=±\frac{{\sqrt{2}}}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,5] | B. | [-1,9] | C. | $[-\frac{1}{2},2]$ | D. | $[\frac{1}{2},3]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com