
(1)求椭圆的离心率e;
(2)设双曲线的离心率为e2,e1+e2=f(a),求f(a)的解析式,并求它的定义域和值域。
| 解:(1)由 ∵ 设A(x1,y1),B(x2,y2) ∴ 且A、B在椭圆 ∴ ②-①:b2(x1-x2)(x1+x2)+a2(y1-y2)(y1+y2)=0
∴ a2=2b2, ∵ a2+b2=c2 ∴ b2=c2 ∴
(2)设椭圆的右准线为l,过N作NN¢^l于N¢, 则由双曲线定义及题意知,
则 由题设知lAB:y=-x+3,代入椭圆方程,消去y得3x2-12x+18-a2=0,
又 ∴ ∴ f(a)的定义域为:
所以f(a)在区间
即 求f(a)的定义域还可以用下面的方法:由M(2,1)在椭圆的内部,e2>1,以及
即 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
已知A、B是椭圆![]() 的一条弦,向量
的一条弦,向量![]() 与AB交于M,且
与AB交于M,且![]() ,以M为焦点,以椭圆的右准线为相应的双曲线与直线AB交于N(4,-1)。
,以M为焦点,以椭圆的右准线为相应的双曲线与直线AB交于N(4,-1)。
(1)求椭圆的离心率e;
(2)设双曲线的离心率为e2,e1+e2=f(a),求f(a)的解析式,并求它的定义域和值域。
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A.k1+k2=k3+k4 | B.k1+k3=k2+k4 |
| C.k1+k2=-(k3+k4) | D.k1+k3=-(k2+k4) |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州中学高三(上)期中数学试卷(理科)(解析版) 题型:选择题
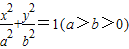 和双曲线
和双曲线 的公共顶点.过坐标原点O作一条射线与椭圆、双曲线分别交于M,N两点,直线MA,MB,NA,NB的斜率分别记为k1,k2,k3,k4,则下列关系正确的是( )
的公共顶点.过坐标原点O作一条射线与椭圆、双曲线分别交于M,N两点,直线MA,MB,NA,NB的斜率分别记为k1,k2,k3,k4,则下列关系正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com