
【题目】如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.

(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() 是
是![]() 的中点,利用
的中点,利用![]() 为线段
为线段![]() 的中点,可得
的中点,可得![]() ,从而可证
,从而可证![]() 平面
平面![]() ;
;
(2)证明![]() ,即可证明
,即可证明![]() 平面
平面![]() .
.
试题解析:
(1)设AC∩BE=O,连接OF,EC.

由于E为AD的中点,
AB=BC=![]() AD,AD∥BC,
AD,AD∥BC,
∴AE∥BC,AE=AB=BC,
因此四边形ABCE为菱形,
∴O为AC的中点.
又F为PC的中点,因此在△PAC中,可得AP∥OF.
又OF平面BEF,AP平面BEF.
∴AP∥平面BEF.
(2)由题意知ED∥BC,ED=BC.
∴四边形BCDE为平行四边形,
因此BE∥CD.
又AP⊥平面PCD,
∴AP⊥CD,
因此AP⊥BE.
∵四边形ABCE为菱形,
∴BE⊥AC.
又AP∩AC=A,AP,AC平面PAC,
∴BE⊥平面PAC.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=2|x﹣1|+x﹣1,g(x)=16x2﹣8x+1.记f(x)≤1的解集为M,g(x)≤4的解集为N.
(1)求M;
(2)当x∈M∩N时,证明:x2f(x)+x[f(x)]2≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级3个班有10名学生在全国英语能力大赛中获奖,学生来源人数如表:
班别 | 高一(1)班 | 高一(2)班 | 高一(3)班 |
人数 | 3 | 6 | 1 |
若要求从10位同学中选出两位同学介绍学习经验,设其中来自高一(1)班的人数为ξ,求随机变量ξ的分布列及数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数![]() ,函数
,函数![]() .
.
(1) 若![]() ,求
,求![]() 的单调递减区间;
的单调递减区间;
(2) 若![]() 为奇函数,且关于
为奇函数,且关于![]() 的不等式
的不等式![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3) 当![]() 时,若方程
时,若方程![]() 有三个不相等的实数根
有三个不相等的实数根![]() 、
、![]() 、
、![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点
(1)求证:AC 1//平面CDB1;(2)求证:AC⊥面BB1C1C ;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品.统计结果如下:
甲流水线样本的频数分布表
产品重量(克) | 频数 |
[490,495) | 6 |
[495,500) | 8 |
[500,505) | 14 |
[505,510) | 8 |
[510,515] | 4 |
乙流水线样本的频率分布直方图
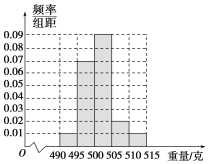
(1)求甲流水线样本合格的频率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
分类 | 甲流水线 | 乙流水线 | 总计 |
合格品 | |||
不合格品 | |||
总计 |
附:K2=![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体ABCDE中,△BCD是边长为2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中点. 
(Ⅰ)求证:BF⊥CD;
(Ⅱ)求二面角C﹣BF﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com