
【题目】从某学校的800名男生中随机抽取50名测量其身高,被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分组:第一组
之间,将测量结果按如下方式分组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4.
,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4.
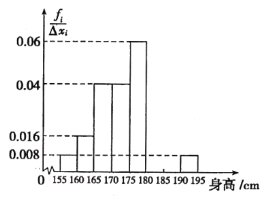
(1)请补全频率分布直方图并求第七组的频率;
(2)估计该校的800名男生的身高的中位数以及身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为![]() ,
,![]() ,事件
,事件![]() ,事件
,事件![]() ,求
,求![]()
【答案】(1)见解析;(2) 中位数为![]() .人数为144人(3)
.人数为144人(3) ![]()
【解析】
(1)由频率分布直方图的性质,即可求解第七组的频率;
(2)根据频率分布直方图,求得各组的频率,再根据频率分布直方图中中位数的计算公式,即可求得中位数,再根据直方图得后三组频率为![]() ,即可求解身高在
,即可求解身高在![]() 以上的人数;
以上的人数;
(3)第六组![]() 的人数为4,设为
的人数为4,设为![]() ,第八组
,第八组![]() 的人数为2,设为
的人数为2,设为![]() ,利用列举法求得基本事件的总数,利用古典概型及其概率的计算公式,求得
,利用列举法求得基本事件的总数,利用古典概型及其概率的计算公式,求得![]() ,进而求得
,进而求得![]() ,最后利用互斥事件的概率加法公式,即可求解.
,最后利用互斥事件的概率加法公式,即可求解.
(1)第六组的频率为![]() ,
,
由频率分布直方图的性质,
可得所以第七组的频率为![]() .
.
(2)身高在第一组![]() 的频率为
的频率为![]() ,
,
身高在第二组![]() 的频率为
的频率为![]() ,
,
身高在第三组![]() 的频率为
的频率为![]() ,
,
身高在第四组![]() 的频率为
的频率为![]() ,
,
由于![]() ,
,![]() ,
,
估计这所学校的![]() 名男生的身高的中位数为m,则
名男生的身高的中位数为m,则![]() ,
,
由![]() ,
,
得![]() ,所以可估计达所学校的
,所以可估计达所学校的![]() 名男生的身高的中位数为
名男生的身高的中位数为![]() ,
,
由直方图得后三组频率为![]() ,
,
所以身高在![]() 以上(含
以上(含![]() )的人数为
)的人数为![]() .
.
(3)第六组![]() 的人数为4,设为
的人数为4,设为![]() ,第八组
,第八组![]() ,的人数为2,
,的人数为2,
设为![]() 则从中选两名男生有
则从中选两名男生有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15种情况.
,共15种情况.
因事件![]() 发生当且仅当随机抽取的两名男生在同一组,所以事件E包含的基本事件为
发生当且仅当随机抽取的两名男生在同一组,所以事件E包含的基本事件为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共7种情况,故
共7种情况,故![]() .
.
由于![]()
![]() ,所以事件
,所以事件![]() 是不可能事件,
是不可能事件,![]() .
.
由于事件E和事件F是互斥事件,所以![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,△PBC为等边三角形,点O为BC的中点,AC⊥PB,平面PBC⊥平面ABC.
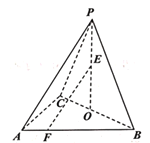
(1)求直线PB和平面ABC所成的角的大小;
(2)求证:平面PAC⊥平面PBC;
(3)已知E为PO的中点,F是AB上的点,AF=![]() AB.若EF∥平面PAC,求
AB.若EF∥平面PAC,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进行理科、文科数学成绩对比,某次考试后,各随机抽取100名同学的数学考试成绩进行统计,其频率分布表如下.
分组 | 频数 | 频率 | 分组 | 频数 | 频率 | |
[135,150] | 8 | 0.08 | [135,150] | 4 | 0.04 | |
[120,135) | 17 | 0.17 | [120,135) | 18 | 0.18 | |
[105,120) | 40 | 0.4 | [105,120) | 37 | 0.37 | |
[90,105) | 21 | 0.21 | [90,105) | 31 | 0.31 | |
[75,90) | 12 | 0. 12 | [75,90) | 7 | 0.07 | |
[60,75) | 2 | 0.02 | [60,75) | 3 | 0.03 | |
总计 | 100 | 1 | 总计 | 100 | 1 |
理科 文科
(Ⅰ)根据数学成绩的频率分布表,求文科数学成绩的中位数的估计值;(精确到0.01)
(Ⅱ)请填写下面的列联表,并根据列联表判断是否有90%的把握认为数学成绩与文理科有关:
数学成绩 | 数学成绩<120分 | 合计 | |
理科 | |||
文科 | |||
合计 | 200 |
参考公式与临界值表: ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程是 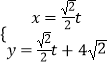 (t是参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.曲线C的极坐标方程为ρ=4cos(θ+
(t是参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.曲线C的极坐标方程为ρ=4cos(θ+ ![]() ).
).
(1)判断直线l与曲线C的位置关系;
(2)过直线l上的点作曲线C的切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象沿
的图象沿![]() 轴向左平移
轴向左平移![]() 个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数
个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数![]() 的图象,对于函数
的图象,对于函数![]() 有以下四个判断:
有以下四个判断:
①该函数的解析式为;![]() ;
;
②该函数图象关于点![]() 对称;
对称;
③该函数在![]() [,上是增函数;
[,上是增函数;
④函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,则
,则![]() .
.
其中,正确判断的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,下列命题正确的有_______.(写出所有正确命题的编号)
,下列命题正确的有_______.(写出所有正确命题的编号)
①![]() 是奇函数;
是奇函数;
②![]() 在
在![]() 上是单调递增函数;
上是单调递增函数;
③方程![]() 有且仅有1个实数根;
有且仅有1个实数根;
④如果对任意![]() ,都有
,都有![]() ,那么
,那么![]() 的最大值为2.
的最大值为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制造两种电子设备:影片播放器和音乐播放器.在每天生产结束后,要对产品进行检测,故障的播放器会被移除进行修复. 下表显示各播放器每天制造的平均数量以及平均故障率.
商品类型 | 播放器每天平均产量 | 播放器每天平均故障率 |
影片播放器 | 3000 | 4% |
音乐播放器 | 9000 | 3% |
下面是关于公司每天生产量的叙述:
①每天生产的播放器有三分之一是影片播放器;
②在任何一批数量为100的影片播放器中,恰好有4个会是故障的;
③如果从每天生产的音乐播放器中随机选取一个进行检测,此产品需要进行修复的概率是0.03.
上面叙述正确的是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点M的极坐标为 ![]() ,圆C的参数方程为
,圆C的参数方程为 ![]() (α为参数).
(α为参数).
(1)直线l过M且与圆C相切,求直线l的极坐标方程;
(2)过点P(0,m)且斜率为 ![]() 的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①命题“若![]() ,则
,则![]() ”的逆否命题为假命题:
”的逆否命题为假命题:
②命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;
”;
③若“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,则
”为假命题,则![]() 为真命题,
为真命题,![]() 为假命题;
为假命题;
④函数![]() 有极值的充要条件是
有极值的充要条件是![]() 或
或![]() .
.
其中正确的个数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com