
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 有区间
有区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围.
的取值范围.
(注:相等的实数根算一个).
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】利用输入语句可以给多个变量赋值,下面能实现这一功能的语句是( )
A.INPUT “A,B,C”a,b,c
B.INPUT “A,B,C=”;a,b,c
C.INPUT a,b,c;“A,B,C”
D.PRINT “A,B,C”;a,b,c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的从高气温,下面的折线代表可能出现的最低气温.
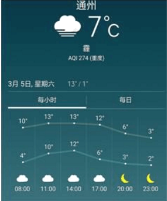
(Ⅰ)指出最高气温与最低气温的相关性;
(Ⅱ)比较最低气温与最高气温方差的大小(结论不要求证明);
(Ⅲ)在![]() 内每个整点时刻的温差(最高气温与最低气温的差)依次记为
内每个整点时刻的温差(最高气温与最低气温的差)依次记为![]() ,求
,求
在连续两个时刻的温差中恰好有一个时刻的温差不小于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计资料,某工艺品厂的日产量最多不超过20件根据统计资料,每日产品废品率![]() 与日产量
与日产量![]() (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率=
(日产品废品率=![]() ×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
×100%) .已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润![]() 日正品赢利额
日正品赢利额![]() 日废品亏损额)
日废品亏损额)
(1)将该车间日利润![]() (千元)表示为日产量
(千元)表示为日产量![]() (件)的函数;
(件)的函数;
(2)当该车间的日产量为多少件时,日利润最大?最大日利润是几千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“m>0,n>0”是“曲线mx2—ny2=1为双曲线”的
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线经过点(0,1),求实数
处的切线经过点(0,1),求实数![]() 的值;
的值;
(Ⅱ)求证:当![]() 时,函数
时,函数![]() 至多有一个极值点;
至多有一个极值点;
(Ⅲ)是否存在实数![]() ,使得函数
,使得函数![]() 在定义域上的极小值大于极大值?若存在,求出
在定义域上的极小值大于极大值?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com