
分析 运用同角的基本关系式,求得cos∠BAC=$\frac{1}{3}$,由条件,结合向量的三角形法则化$\overrightarrow{AD}•\overrightarrow{BC}$=-$\frac{1}{4}$$\overrightarrow{AB}$2+$\frac{3}{4}$$\overrightarrow{AC}$2-$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AC}$,再由向量数量积的定义和性质,向量的平方即为模的平方,计算即可得到所求值.
解答  解:△ABC中,AB=2,AC=3,tan∠BAC=2$\sqrt{2}$,
解:△ABC中,AB=2,AC=3,tan∠BAC=2$\sqrt{2}$,
由sin2∠BAC+cos2∠BAC=1,
tan∠BAC=$\frac{sin∠BAC}{cos∠BAC}$,
解得cos∠BAC=$\frac{1}{3}$,
D是BC边上的点,且BD=3CD,
可得$\overrightarrow{AD}•\overrightarrow{BC}$=($\overrightarrow{AB}$+$\overrightarrow{BD}$)•($\overrightarrow{AC}$-$\overrightarrow{AB}$)
=($\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{BC}$)•($\overrightarrow{AC}$-$\overrightarrow{AB}$)=($\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$)•($\overrightarrow{AC}$-$\overrightarrow{AB}$)
=-$\frac{1}{4}$$\overrightarrow{AB}$2+$\frac{3}{4}$$\overrightarrow{AC}$2-$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AC}$=-$\frac{1}{4}$×4+$\frac{3}{4}$×9-$\frac{1}{2}$×2×3×$\frac{1}{3}$=$\frac{19}{4}$.
故答案为:$\frac{19}{4}$.
点评 本题考查向量在三角形中的应用,考查向量的加减运算和数量积的定义及性质,主要是向量的平方即为模的平方,考查同角的基本关系式的运用,以及运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|x≠5} | B. | {x|x=5} | C. | {x|x<5} | D. | {x|x>5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
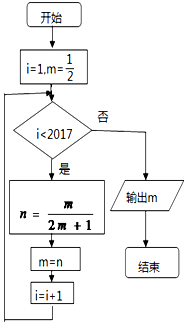
| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{4032}$ | D. | $\frac{1}{4034}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{x={t^2}}\\{y={t^4}}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=sint}\\{y={{sin}^2}t}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=t}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=t}\\{y={t^2}}\end{array}}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由 ${a_1}=1,{a_{n+1}}=\frac{a_n}{{1+{a_n}}}$,因为${a_1}=1,{a_2}=\frac{1}{2},{a_3}=\frac{1}{3},{a_4}=\frac{1}{4}$,故有${a_n}=\frac{1}{n}(n∈{N^*})$ | |
| B. | 科学家利用鱼的沉浮原理制造潜艇 | |
| C. | 妲己惑纣王,商灭;西施迷吴王,吴灭;杨贵妃迷唐玄宗,致安史之乱,故曰:“红颜祸水也” | |
| D. | 《论语•学路》篇中说:“名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所措手足;所以,名不正,则民无所措手足”. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com