
如图所示,直三棱柱ABCA1B1C1中,D、E分别是AB、BB1的中点,AA1=AC=CB=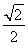 AB.
AB.
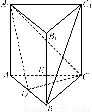
(1)证明:BC1∥平面A1CD;
(2)求二面角DA1CE的正弦值..
(1)见解析(2)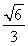
【解析】(1)证明:连结AC1交A1C于点F,则F为AC1中点.又D是AB中点,连结DF,则BC1∥DF.
因为DF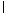 ?平面A1CD,BC1
?平面A1CD,BC1 平面A1CD,所以BC1∥平面A1CD.
平面A1CD,所以BC1∥平面A1CD.
(2)由AC=CB=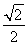 AB得AC⊥BC.以C为坐标原点,
AB得AC⊥BC.以C为坐标原点,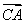 的方向为x轴正方向,建立如图所示的空间直角坐标系Cxyz.
的方向为x轴正方向,建立如图所示的空间直角坐标系Cxyz.
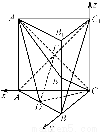
设CA=2,则D(1,1,0),E(0,2,1),A1(2,0,2),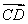 =(1,1,0),
=(1,1,0),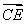 =(0,2,1),
=(0,2,1),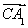 =(2,0,2).
=(2,0,2).
设n=(x1,y1,z1)是平面A1CD的法向量,则 即
即
可取n=(1,-1,-1).
同理,设m为平面A1CE的法向量,则 可取m=(2,1,-2).
可取m=(2,1,-2).
从而cos〈n,m〉=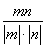 =
=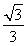 ,故sin〈n,m〉=
,故sin〈n,m〉=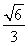 .即二面角D-A1C-E的正弦值为
.即二面角D-A1C-E的正弦值为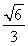


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第4课时练习卷(解析版) 题型:填空题
设a,b>0,且ab=1,不等式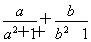 ≤λ恒成立,则λ的取值范围是________.
≤λ恒成立,则λ的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:填空题
已知实数x、y满足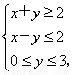 则z=2x+y的最小值是________.
则z=2x+y的最小值是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第1课时练习卷(解析版) 题型:解答题
已知关于x的不等式: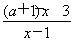 <1.
<1.
(1)当a=1时,解该不等式;
(2)当a>0时,解该不等式.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
如图,在三棱柱ABCA1B1C1中,A1B⊥平面ABC,AB⊥AC,且AB=AC=A1B=2.
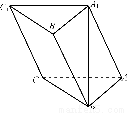
(1)求棱AA1与BC所成的角的大小;
(2)在棱B1C1上确定一点P,使二面角P-AB-A1的平面角的余弦值为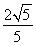 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
如右图,在棱长为a的正方体ABCDA1B1C1D1中,G为△BC1D的重心,
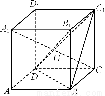
(1)试证:A1、G、C三点共线;
(2)试证:A1C⊥平面BC1D;
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:填空题
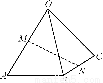
已知空间四边形OABC,点M、N分别是OA、BC的中点,且 =a,
=a,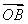 =b,
=b,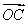 =c,用a,b,c表示向量
=c,用a,b,c表示向量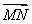 =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:填空题
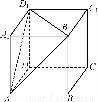
如图所示,正方体ABCDA1B1C1D1的棱长为6,则以正方体ABCDA1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:填空题
P为△ABC所在平面外一点,O为P在平面ABC内的射影.
(1)若P到△ABC三边距离相等,且O在△ABC的内部,则O是△ABC的________心;
(2)若PA⊥BC,PB⊥AC,则O是△ABC的________心;
(3)若PA,PB,PC与底面所成的角相等,则O是△ABC的________心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com