
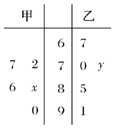
 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);分析 (1)由平均分相等求出a=3,由此能求出甲的方差和乙的方差,由$\overline x$甲=$\overline x$乙,${{S}_{甲}}^{2}$<${{S}_{乙}}^{2}$,求出从成绩的稳定性角度考虑,派甲参加培训比较合适.
(2)利用列举法求出从甲的成绩中任取两次的所有结果和至少有一次成绩在(90,100]之间的所有结果,由此能求出在抽取的成绩中,至少有一次成绩在(90,100]之间的概率.
解答 解 (1)由平均分相等得:
$\overline x$甲=$\frac{88-89-90-91+92}{5}$=$\overline x$乙=$\frac{84+88+89+(90+a)+96}{5}$=90,
解得a=3.
∴甲的方差:${{S}_{甲}}^{2}$=$\frac{1}{5}$[(88-90)2+(89-90)2+(90-90)2+(91-90)2+(92-90)2]=2,
乙的方差${{S}_{乙}}^{2}$=$\frac{1}{5}$[(84-90)2+(88-90)2+(80+90)2+(93-90)2+(96-90)2]=17.2,
因为$\overline x$甲=$\overline x$乙,${{S}_{甲}}^{2}$<${{S}_{乙}}^{2}$,
所以从成绩的稳定性角度考虑,派甲参加培训比较合适.
(2)从甲的成绩中任取两次的所有结果有:
(88,89),(88,90),(88,91)(88,92),(89,90),(89,91),(89,92),
(90,91),(90,92),(91,92),共10种;
其中至少有一次成绩在(90,100]之间的所有结果有:
(88,91),(88,92),(89,91),(89,92),(90,91),
(90,92),(91,92)共7种.
所以在抽取的成绩中,至少有一次成绩在(90,100]之间的概率P=$\frac{7}{10}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
 航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时.飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,求山顶的海拔高度(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$).
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时.飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,求山顶的海拔高度(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
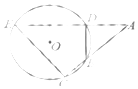 如图,圆O的弦ED,CB的延长线交于点A.若BD⊥AE,AB=4,BC=2,AD=3,则DE= ;CE= .( )
如图,圆O的弦ED,CB的延长线交于点A.若BD⊥AE,AB=4,BC=2,AD=3,则DE= ;CE= .( )| A. | 5、2$\sqrt{7}$ | B. | 5、7$\sqrt{7}$ | C. | 7 7$\sqrt{2}$ | D. | 5、$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2016,0) | B. | (-∞,-2017) | C. | (-∞,-2016) | D. | (-2016,-2015) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y+1=0 | B. | x+y-2=0 | C. | x-y+2=0 | D. | x-y-1=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com