
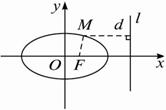
解析:设d是点M到直线l:x=![]() 的距离,?
的距离,?
根据题意,点M的轨迹就是集合P={M|![]() =
=![]() },??
},??
由此得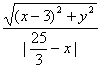 =
=![]() .
.
将上式两边平方,并化简,得16x2+25y2=400,
即![]() +
+![]() =1.?
=1.?
所以点M的轨迹是长轴、短轴长分别为10、8的椭圆.?
温馨提示:椭圆![]() +
+![]() =1的离心率为e=
=1的离心率为e=![]() .通过此例可以看出椭圆
.通过此例可以看出椭圆![]() +
+![]() =1上任意一点M到焦点F(3,0)的距离与M到直线l:x=
=1上任意一点M到焦点F(3,0)的距离与M到直线l:x=![]() 的距离的比值为离心率e.一般地,?点M(x,y)与定点F(c,0)的距离和它到定直线l:x=
的距离的比值为离心率e.一般地,?点M(x,y)与定点F(c,0)的距离和它到定直线l:x=![]() 的距离的比是常数
的距离的比是常数![]() (a>c>0),点M的轨迹是椭圆,其方程为
(a>c>0),点M的轨迹是椭圆,其方程为![]() +
+![]() =1(b2=a2-c2).因此,椭圆可以看作动点M到定点F的距离与它到定直线的距离的比为常数e(0
=1(b2=a2-c2).因此,椭圆可以看作动点M到定点F的距离与它到定直线的距离的比为常数e(0


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
点M(x,y)与定点F(1,0)的距离比它到直线x=8的距离大1, 则动点M的轨迹方程为 ( ).
A. y2=16(x-5) B. x2=16(y-5)
C. x2=-16(y-5) D. y2=-16(x-5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com