练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量m＝（cosx，sinx），n＝（cosx，cosx）（x∈R），设函数f（x）＝m·n

    （1）求 f（x）的解析式，并求最小正周期．

    （2）若函数 g（x）的图像是由函数 f（x）的图像向右平移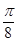个单位得到的，求g（x）的最大值及使g（x）取得最大值时x的值．

     

    【答案】

    （1），最小正周期为；

    （2）时

    【解析】本试题主要是考查了三角函数的性质的运用。

    （1）因为向量m＝（cosx，sinx），n＝（cosx，cosx）（x∈R），则函数f（x）＝m·n

    可以运用向量的数量积表示为单一三角函数，并求解周期。

    （2）当将函数 g（x）的图像是由函数 f（x）的图像向右平移个单位得到的，利用三角函数的性质得到最值。

    解：（1）

    （x∈R）

    ∴f（x）的最小正周期为

    （2）

    ∴当，即时

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2010-2011学年湖南省长沙市高三第六次月考理科数学卷 题型：解答题

    (本小题满分12分)

    已知向量m＝(sin，1)，n＝(cos，cos2)，f(x)＝m·n.

    (1)若f(x)＝1，求cos(－x)的值；

    (2)在△ABC中，角A，B，C的对边分别是a，b，c且满足acosC＋c＝b，求函数f(B)的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量m＝（sin，1），n＝（cos，cos2），f（x）＝m·n．

       （1）若f（x）＝1，求cos（－x）的值；

       （2）在△ABC中，角A，B，C的对边分别是a，b，c且满足acosC＋c＝b，求函数f（B）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量m＝(sin，1)，n＝(cos，cos2)，f(x)＝m·n.

    (1)若f(x)＝1，求cos(x＋)的值；

    (2)在△ABC中，角A，B，C的对边分别是a，b，c且满足acosC＋c＝b，求函数f(B)的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，角A，B，C的对边分别为a，b，c.已知向量m＝，n＝，m·n＝－1.

    (1)求cos A的值；

    (2)若a＝2，b＝2，求c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，a、b、c分别是角A、B、C的对边，已知向量m＝(a，b)，向量n＝(cos A，cos B)，向量p＝(2sin，2sin A)，若m∥n，p2＝9，求证：△ABC为等边三角形．

    查看答案和解析>>

    同步练习册答案