
【题目】“双11”促销活动中,某商场为了吸引顾客,搞好促销活动,采用“双色球”定折扣的方式促销,即:在红、黄的两个纸箱中分别装有大小完全相同的红、黄球各5个,每种颜色的5个球上标有1,2,3,4,5等5个数字,顾客结账时,先分别从红、黄的两个纸箱中各取一球,按两个球的数字之和为折扣打折,如![]() ,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
,就按3折付款,并规定取球后不再增加商品.按此规定,顾客享有6折及以下折扣的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长AB=3,侧棱AA1=2,E是棱CC1的中点,点F满足![]() =2
=2![]() .
.
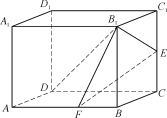
(1)求异面直线FE和DB1所成角的余弦值;
(2)记二面角E-B1F-A的大小为θ,求|cosθ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果一个数列从第2项起,每一项与它前一项的差都大于或等于2,则称这个数列为“D数列”.
(1)若首项为1的等差数列![]() 的每一项均为正整数,且数列
的每一项均为正整数,且数列![]() 为“D数列”,其前n项和
为“D数列”,其前n项和![]() 满足
满足![]() (
(![]() ),求数列
),求数列![]() 的通项公式;
的通项公式;
(2)已知等比数列![]() 的每一项均为正整数,且数列
的每一项均为正整数,且数列![]() 为“D数列”,
为“D数列”,![]() ,设
,设 (
(![]() ),试判断数列
),试判断数列![]() 是否为“D数列”,并说明理由.
是否为“D数列”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题14分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.
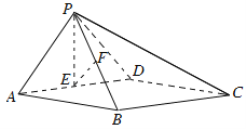
(Ⅰ)求证:PE⊥BC;
(Ⅱ)求证:平面PAB⊥平面PCD;
(Ⅲ)求证:EF∥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱![]() 中,
中,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 平面
平面![]()
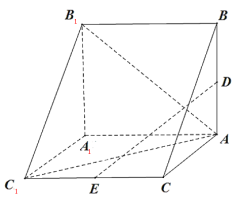
(1) 证明:![]() 是
是![]() 的中点;
的中点;
(2) 设![]() ,四边形
,四边形![]() 为边长为4正方形,四边形
为边长为4正方形,四边形![]() 为矩形,且异面直线
为矩形,且异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,求该三棱柱
,求该三棱柱![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】淮北市第一次模拟考试理科共考语文、数学、英语、物理、化学、生物六科,安排在某两日的四个半天考完,每个半天考一科或两科.若语文、数学、物理三科中任何两科不能排在同一个半天,则此次考试不同安排方案的种数有( )(同一半天如果有两科考试不计顺序)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() 和椭圆
和椭圆![]() :
:![]() 的焦点且方向向量为
的焦点且方向向量为![]() ,且椭圆
,且椭圆![]() 的中心关于直线
的中心关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() 、
、![]() ,且满足
,且满足![]() (
(![]() 为原点)?若存在,求直线
为原点)?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
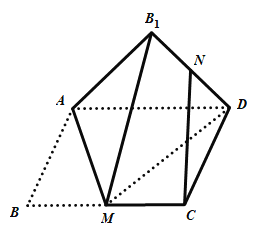
A.存在某个位置,使得![]()
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]()
D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com