
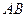 宽2m,渠
宽2m,渠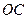 深为1.5m,水面EF距AB为0.5m. (1)求截面图中水面宽度;
深为1.5m,水面EF距AB为0.5m. (1)求截面图中水面宽度;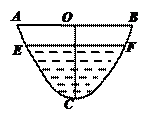 (2)由于情况有变,现要将此水渠改造为横截面是等腰梯形,要求渠深不变,不准往回填土,只准挖土,试求截面梯形的下边长为多大时,才能使所挖的土最少?
(2)由于情况有变,现要将此水渠改造为横截面是等腰梯形,要求渠深不变,不准往回填土,只准挖土,试求截面梯形的下边长为多大时,才能使所挖的土最少?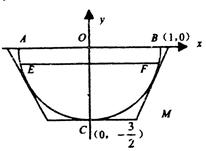
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源:不详 题型:单选题
| A.2007 | B.2008 | C.2009 | D.2010 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
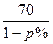 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
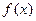 ,有下述四个命题,其中正确命题为( )
,有下述四个命题,其中正确命题为( )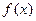 是奇函数,则
是奇函数,则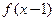 的图象关于点A(1,0)对称;
的图象关于点A(1,0)对称; 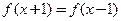 ,则
,则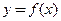 的图象关于直线
的图象关于直线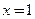 对称;
对称; 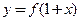 为偶函数,则
为偶函数,则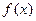 的图象关于直线
的图象关于直线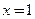 对称;
对称;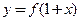 与函数
与函数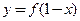 的图象关于直线
的图象关于直线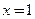 对称。
对称。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
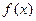 的定义域为
的定义域为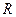 ,若存在常数
,若存在常数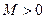 ,使
,使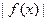 ≤
≤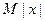 对一切实数
对一切实数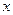 均成立,则称
均成立,则称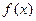 为“倍约束函数”.现给出下列函数:
为“倍约束函数”.现给出下列函数: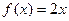 ;
;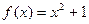 ;
;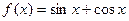 ;
;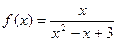 ;
;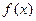 是定义在实数集
是定义在实数集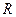 上的奇函数,且对一切
上的奇函数,且对一切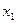 ,
,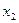 均有
均有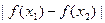 ≤
≤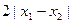 .其中是“倍约束函数”的有 ( )
.其中是“倍约束函数”的有 ( )A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com