在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱AB,CC1,D1A1,BB1的中点.
(1)证明:FH∥平面A1EG;
(2)证明:AH⊥EG;
(3)求三棱锥A1-EFG的体积.
分析:(1)根据正方体的几何特征,我们易证明FH∥A1G,结合线面平行的判定定理,即可得到FH∥平面A1EG;
(2)根据正方体的几何特征,易得AH⊥A1G,AH⊥A1E,结合线面垂直的判定定理,即可得到AH⊥平面A1EG,再由线面垂直的性质,即可得到AH⊥EG;
(3)连接HA1,HE,HG,结合(1)的结论可得VH-A1EG=VF-A1EG,求出棱锥的底面面积和高后,代入棱锥体积公式即可得到答案.
解答: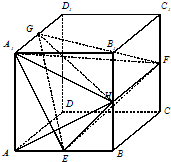
解:(1)证明:∵FH∥B
1C
1,B
1C
1∥A
1G,∴FH∥A
1G
又A
1G?平面A
1GE,FH?平面A
1GE,∴FH∥平面A
1EG
(2)∵A
1G⊥平面ABB
1A
1,AH?平面ABB
1A
1,∴AH⊥A
1G
又∵△ABH≌△A
1AE,∴∠HAB=∠EA
1A∵∠A
1AH+∠HAB=90°,∴∠A
1AH+∠EA
1A=90°,∴AH⊥A
1E
又∵A
1G∩A
1E=A
1,∴AH⊥平面A
1EG,∵EG?平面A
1EG,故AH⊥EG
(3)连接HA
1,HE,HG,由(1)得FH∥平面A
1EG,∴
VH-A1EG=VF-A1EG又
S△A1EH=SABB1A1-S△A1AE-S△A1B1H-S△EBH=1×1---=,
A1G=∴
VA1-EFG=VF-A1EG=VH-A1EG=VG-A1EH=S△A1EH•A1G=××= 点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定及性质,棱锥的体积,熟练掌握空间直线与平面平行或垂直关系的判定、性质、定义,是解答本题的关键.

 解:(1)证明:∵FH∥B1C1,B1C1∥A1G,∴FH∥A1G
解:(1)证明:∵FH∥B1C1,B1C1∥A1G,∴FH∥A1G

 在线段AD1上运动,给出以下四个命题:
在线段AD1上运动,给出以下四个命题: (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.
(2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.