已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为 .求过点A(-5,2),且在x轴y轴上截距相等的直线方程 .
【答案】
分析:由斜率公式和直线平行的条件可得m的值;注意分直线过不过原点来考虑,防止漏解.
解答:解:直线2x+y-1=0的斜率为-2,
故

=-2,解得m=-8;
当直线过原点时,可设方程为y=kx,
代入点(-5,2),可得k=
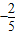
,
故方程为y=
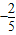
x,即2x+5y=0,
当直线不过原点时,设为
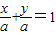
,
代入点(-5,2),可得a=-3,
故方程为:x+y+3=0
故答案为:-8,2x+5y=0或x+y+3=0
点评:本题考查直线的斜率公式和直线方程的截距式,属基础题.

 阅读快车系列答案
阅读快车系列答案