
分析 先求导数$f′(x)=\frac{a}{x}+2(x+1)$,根据条件可得到$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}>4$,从而根据导数的定义便可得到$\frac{a}{x}+2(x+1)>4$,这样便可得到a>-2x2+2x,容易求出二次函数y=-2x2+2x在(0,+∞)上的最大值,从而便可得出实数a的取值范围.
解答 解:$f′(x)=\frac{a}{x}+2(x+1)$;
∵x1>x2;
∴x1-x2>0;
∴由f(x1)-f(x2)>4(x1-x2)得,$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}>4$;
∴$\frac{a}{x}+2(x+1)>4$;
∴a>-2x2+2x恒成立;
$-2{x}^{2}+2x=-2(x-\frac{1}{2})^{2}+\frac{1}{2}≤\frac{1}{2}$;
∴$a>\frac{1}{2}$;
∴实数a的取值范围为($\frac{1}{2},+∞$).
故答案为:$(\frac{1}{2},+∞)$.
点评 考查函数导数的定义,配方法求二次函数的最值,以及关于恒成立问题的处理方法,要正确求导.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:解答题
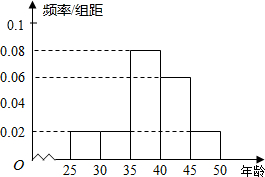
| 组别 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 50 | 50 | a | 150 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a3>0,则a2015<0 | B. | 若a4>0,则a2015<0 | ||
| C. | 若a3>0,则a2015>0 | D. | 若a4>0,则a2015>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
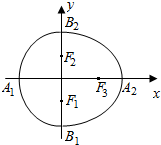 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )| A. | 5,4 | B. | $\sqrt{3}$,1 | C. | 5,3 | D. | $\frac{\sqrt{7}}{2}$,1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com