
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数字-1,0,1,2.称“从盒中随机抽取一张,记下卡片上的数字后并放回”为一次试验(设每次试验的结果互不影响).
(1)在一次试验中,求卡片上的数字为正数的概率;
(2)在四次试验中,求至少有两次卡片上的数字都为正数的概率;
(3)在两次试验中,记卡片上的数字分别为X,η,试求随机变量X=X·η的分布列与数学期望E(X).
(1)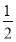 (2)
(2)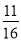 (3)
(3)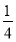
【解析】(1)记事件A为“在一次试验中,卡片上的数字为正数”,则P(A)=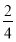 =
=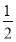 .
.
(2)记事件B为“在四次试验中,至少有两次卡片上的数字都为正数”.由(1)可知在一次试验中,卡片上的数字为正数的概率是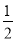 .所以P(B)=1-
.所以P(B)=1-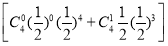 =
=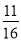 .
.
(3)由题意可知,X,η的可能取值都为-1,0,1,2,
所以随机变量X的可能取值为-2,-1,0,1,2,4.
P(X=-2)=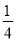 ×
× ×2=
×2=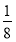 ;
;
P(X=-1)= ×
× ×2=
×2=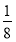 ;
;
P(X=0)=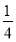 ×
×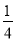 ×7=
×7=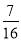 ;
;
P(X=1)= ×
×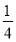 ×2=
×2=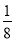 ;
;
P(X=2)=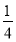 ×
× ×2=
×2=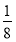 ;
;
P(X=4)= ×
× =
=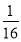 .
.
所以随机变量X的分布列为
X | -2 | -1 | 0 | 1 | 2 | 4 |
P |
|
|
|
|
|
|
所以E(X)=-2×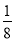 -1×
-1× +0×
+0×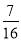 +1×
+1×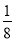 +2×
+2×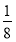 +4×
+4×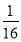 =
=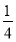 .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x6练习卷(解析版) 题型:选择题
f(x)= 则下列关于y=f[f(x)]-2的零点个数判断正确( ).
则下列关于y=f[f(x)]-2的零点个数判断正确( ).
A.当k=0时,有无数个零点,
B.当k<0时,有3个零点
C.当k>0时,有3个零点
D.无论k取何值,都有4个零点
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x1练习卷(解析版) 题型:填空题
给出下列命题:
①抛物线x=- y2的准线方程是x=1;
y2的准线方程是x=1;
 ②若x∈R,则
②若x∈R,则 的最小值是2;
的最小值是2;
③ sin xdx=2;
④若X~N(3,σ2)且P(0≤X≤3)=0.4,则P(X≥6)=0.1.
其中正确的是(填序号)________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-d4练习卷(解析版) 题型:解答题
已知函数f(x)= .
.
(1)函数f(x)在点(0,f(0))的切线与直线2x+y-1=0平行,求a的值;
(2)当x∈[0,2]时,f(x)≥ 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-d3练习卷(解析版) 题型:解答题
如图,在矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将△AOD折起,使DB= .
.

(1)求证:平面AOD⊥平面ABCO;
(2)求直线BC与平面ABD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练2-1练习卷(解析版) 题型:解答题
已知m=(2cos x+2 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)将y表示为x的函数f(x),并求f(x)的单调增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-9练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,设抛物线y2=4x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的倾斜角为120°,那么|PF|=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-9练习卷(解析版) 题型:填空题
过双曲线 =1的右焦点,且平行于经过一、三象限的渐近线的直线方程是________.
=1的右焦点,且平行于经过一、三象限的渐近线的直线方程是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-6练习卷(解析版) 题型:填空题
设Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列,且a2+a5=2am,则m=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com