
分析 利用二分法求方程的近似解的方法把区间一次次缩小,一直缩小到答案找出为止即可.
解答 解:由已知令f(x)=2x-x3,
∵f(2)<0,f(1)>0,方程2x-x3=0的x∈(1,2)
由二分法知计算f(1.5)>0,方程2x-x3=0的x∈(1.5,2),
由二分法知计算f(1.75)<0,方程2x-x3=0的x∈(1.5,1.75),
由二分法知计算f(1.625)<0,方程2x-x3=0的x∈(1.5,1.625),
由二分法知计算f(1.5625)<0,方程2x-x3=0的x∈(1.5,1.5625),
由二分法知计算f(1.53125)<0,方程2x-x3=0的x∈(1.5,1.53125),
故符合要求的选项只有1.5.
故答案为:1.5.
点评 本题主要考查用二分法求区间根的问题,属于基础题型.在利用二分法求区间根的问题上,如果题中有根的精确度的限制,在解题时就一定要计算到满足要求才能结束.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
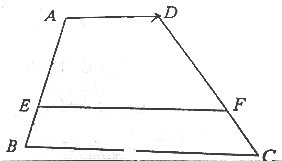 如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.
如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com